查找
查找
16:46 在闷热了许久之后,终于有丝丝凉意袭来。
1.符号表
关于查找算法,我们需要研究的第一个数据结构便是符合表,对其最通俗易懂的解释则是:一个key-value形式的映射关系,字典。
api
一个简单的符号表api:
package define;
public interface SimpleST<Key, Value> {
void put(Key key, Value value);
Value get(Key key);
void delete(Key key);
boolean contains(Key key);
boolean isEmpty();
int size();
Iterable<Key> keys();
}
一个简单的有序符号表api:
package define;
public interface SimpleOrderST<Key extends Comparable<Key>,Value> {
void put(Key key, Value value);
Value get(Key key);
void delete(Key key);
boolean contains(Key key);
boolean isEmpty();
int size();
Key min();
Key max();
Key floor(Key key);//小于等于key的最大键
Key ceiling(Key key);//大于等于key的最小键
int rank(Key key);//小于key的键的数量
Key select(int k);//排名为k 的键
}
关于符号表的一些细节,诸如:null key,null value,重复的key,key的等价性等诸多细节,还是得看书上…
用例
在学习符号表的具体实现之前,先给一个符号表的用例,毕竟 影响我们具体实现的最大因素便是我们对将要实现的东西的理解程度(功能决定形态?🤣)。
package define;
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class FrequencyCounter {
public static void main(String[] args) {
int minLen = Integer.parseInt(args[0]);
SimpleST<String, Integer> st ;// todo 待具体实现
while (!StdIn.isEmpty()) {
String word = StdIn.readString();
if (word.length() < minLen) continue;
if (!st.contains(word)) {
st.put(word, 1);
} else {
st.put(word, st.get(word) + 1);
}
}
String max = "";
st.put(max, 0);
for (String word : st.keys()) {
if (st.get(word) > st.get(max)) max = word;
}
StdOut.println(max + " " + st.get(max));
}
}
实现之无序链表
使用链表来实现符号表,其中每对 k-v 就是链表中的一个node
show me code:
package define;
/**
* 基于链表的无序符号表实现
* @param <Key>
* @param <Value>
*
* @author liaozk
*/
public class SequentialSearchST<Key,Value> implements SimpleST<Key,Value> {
private Node frist;
int size = 0;
private class Node {
Key key;
Value val;
Node next;
public Node(Key key,Value val,Node next) {
this.key = key;
this.val = val;
this.next = next;
}
}
@Override
public void put(Key key, Value value) {
//依据前面的介绍,此处put要干的操作就是:
//1.如果列表存在,则将value更新
//2.如果列表不存在,则插入
//2.1.关于插入的实现,可以选择每次进入到链表的末尾,然后挂一个元素删去,这是如此的符合直觉
//2.2.不过我的朋友,当然也可以将现有的frist挂在新元素上,这是如此的优雅
//3.每次看书中对于for循环的使用都会让我再一次怀疑自己,是否理解了for 语法,每次的结果都是no
for (Node x = frist; x != null; x = x.next) {
if (key.equals(x.key)) {
x.val = value;
return;
}
}
//没找到,最前面加一个node
frist = new Node(key, value, frist);
size += 1;
}
@Override
public Value get(Key key) {
for (Node x = frist; x != null; x = x.next) {
if (key.equals(x.key)) {
return x.val;
}
}
return null;
}
@Override
public void delete(Key key) {
if (key.equals(frist.key)) {
frist = frist.next;
size -= 1;
return;
}
for (Node x = frist; x.next != null; x = x.next) {
if (key.equals(x.next.key)) {
Node target = x.next;
x.next = target.next;
size -= 1;
return;
}
}
}
@Override
public int size() {
return size;
}
@Override
public Iterable<Key> keys() {
//这里我们使用第一章中创建的listqueue来实现
ListQueue<Key> queue = new ListQueue<>();
for (Node x = frist; x.next != null; x = x.next) {
queue.enqueue(x.key);
}
return queue;
}
}
无序链表实现的性能分析
我想《算法》之所以为经典,不同于网上随处可见的各类n万字的算法笔记的关键之处便在于其对“某种”思维的培养。如果你并不觉得我们需要更快的实现,那么我们就先来探索一下当前实现的性能。
我这里仅仅只是将输出嵌套进入了代码中,没有将其分离出来,故也就不展示代码了,结论便是:
在tale样本中对长度大于8的单词进行统计的过程中:times:9208,cur:9207,sum:42389028,agv:4603
平均每一次的put需要访问4000多个node…
实现之有序数组
使用的数据结构是一对平行的数组,一个储存键,一个储存值。在有序的符号表api中,我们需要理解的核心便是
key = select(rank(key))
i = rank(select(i))
Show me code:
package define;
public class BinarySearchOrderST<Key extends Comparable<Key>, Value> implements SimpleOrderST<Key,Value> {
private Key[] keys;
private Value[] values;
private int n;
public BinarySearchOrderST(int capacity) {
keys = (Key[]) new Comparable[capacity];
values = (Value[]) new Object[capacity];
}
@Override
public void put(Key key, Value value) {
int i = rank(key);
if (i < n && keys[i].compareTo(key) == 0) {
values[i] = value;
return;
}
for (int j = n; j > i; j--) {
keys[j] = keys[j-1];
values[j] = values[j-1];
}
keys[i] = key;
values[i] = value;
}
@Override
public Value get(Key key) {
if (isEmpty()) return null;
int i = rank(key);
if (i < n && keys[i].compareTo(key) == 0) {
return values[i];
} else {
return null;
}
}
@Override
public void delete(Key key) {
int i = rank(key);
if (keys[i].compareTo(key) == 0) {
for (int j = i; j < n; j++) {
keys[j] = keys[j+1];
values[j] = values[j+1];
}
keys[n] = null;
values[n] = null;
} else {
throw new RuntimeException("not contains such key");
}
}
@Override
public int size() {
return n;
}
@Override
public Key min() {
return keys[0];
}
@Override
public Key max() {
return keys[n];
}
@Override
public Key floor(Key key) {
int i = rank(key);
if (keys[i].compareTo(key) == 0) {
return keys[i];
} else {
return keys[i-1];
}
}
@Override
public Key ceiling(Key key) {
return keys[rank(key)];
}
//此处rank 就是一个二分查找,我们可以递归实现,也可以迭代实现
//先吃一个迭代的
//rank在此处的要求:返回表中小于key的键的数量
/*
* key在表中,有三种可能性
* 等于
* 大于:lo会增长到 n
* 小于:lo = 0
* 所以lo永远是比key小的元素的个数
* */
@Override
public int rank(Key key) {
int lo = 0,hi = n-1;
while (lo <= hi) {
int mid = lo + (hi-lo)/2;
if (key.compareTo(keys[mid]) < 0) {
hi = mid - 1;
} else if (key.compareTo(keys[mid]) > 0) {
lo = mid + 1;
} else {
return mid;
}
}
return lo;//思考为何是lo
}
//吃完迭代,吃递归
public int rank1(Key key) {
return rank2(0, n-1, key);
}
private int rank2(int lo, int hi, Key key) {
if (lo > hi) return lo;
int mid = lo + (hi - lo)/2;
int cmp = key.compareTo(keys[mid]);
if (cmp < 0) {
return rank2(lo, mid-1, key);
} else if (cmp > 0) {
return rank2(mid + 1, hi,key);
} else {
return mid;
}
}
@Override
public Key select(int k) {
return keys[k];
}
}
2.二叉查找树
Binary Search Trees
前面的符号表的有序数组实现,面临的一个巨大问题便是每次插入,除了考虑扩容等之外,还需要额外考虑插入/删除 中间元素时的数组整体移动。
二叉查找树便是有序数组的查找高效与链表结构的灵活性相结合的高效产物。
在介绍二叉查找树前,先给一些基础的定义:
What Is Tree:
-
A set of nodes;
-
A set of edges that connect those nodes(only one path exists between two nodes);
-
总结:点&边的集合,其中两个点之间只有一条路径。一个点&边构成的没有环的东西。
Rooted Tree:
-
one node is root;
-
Every node have only one parent except root;
-
no child node is leaf;
-
总结:树的基础上,有一个根节点,除了根节点其余节点只有一个父节点
Rooted Binary Trees:
-
every node has either 0,1 or 2 children;
-
总结:根树的基础上进一步限制了 子节点的数量
Binary Search Trees:
-
Left means less,Right means greater;
-
can`t have duplicate key;
-
根二叉树的基础上进一步限制了,左右子节点,无重复key 可以将一颗完全bst想象成,用手将一串排好序的元素从中间一把抓起来。
这里的进化逻辑就是:树 -> 根树 -> 根二叉树 -> 二叉搜索树
show me code
Tips:在用到一些递归场景的时候,注意 arms-length base case
BSTMap
package define;
import define.impl.ListQueue;
public class BSTMap<Key extends Comparable<Key>, Value> implements SimpleOrderST<Key,Value> {
private Node root;
private class Node {
private Key key;
private Value val;
private Node left,right;
private int n;//以该节点作为根的子树的节点数量。为什么要这个东西呢?
public Node (Key key, Value val,int n) {
this.key = key;
this.val = val;
this.n = n;
}
}
/*
* 我们对put方法的要求
* 1.key 存在就将其val 更新为 value
* 2.key 不存在,在合适的位置新增一个key
* 难点:如何实现插入,如何在递归的过程中获取上一个元素
* 如何去理解递归及递归与迭代之间的转换是学习整个算法过程中的一个持久主题吧,一个值得大量刻意练习的主题
*/
@Override
public void put(Key key, Value value) {
root = put(root, key, value);
}
private Node put(Node cur, Key key, Value value) {
if (cur == null) return new Node(key, value, 1);
int com = key.compareTo(cur.key);
if (com > 0 ) {
cur.right = put(cur.right, key, value);
} else if (com < 0) {
cur.left = put(cur.left, key, value);
} else {
cur.val = value;
}
cur.n = size(cur.left) + size(cur.right) + 1;
return cur;
}
/*
我们对 get方法的要求
1.二分查找的递归实现
*/
@Override
public Value get(Key key) {
Node ta = get(root, key);
if (ta == null) {
return null;
} else {
return ta.val;
}
}
private Node get(Node node,Key key) {
if (node == null) return null;
int cmp = key.compareTo(node.key);
if (cmp > 0) {
return get(node.right, key);
} else if (cmp < 0) {
return get(node.left, key);
} else {
return node;
}
}
/**
* 关于delete更加优雅的实现
* 1.如果目标结点只有一个子结点,则用其子结点替换目标结点
* 2.如果两个都有则找最接近的(最小大/最大小)
* @param key
*/
@Override
public void delete(Key key) {
}
private Node delete(Node x, Key key) {
if (x == null) return null;
int cmp = key.compareTo(x.key);
Node maxMin = x;
if (cmp > 0) {
x.right = delete(x.right, key);
} else if (cmp < 0) {
x.left = delete(x.left, key);
} else {
//x就是我们要删除的元素
if (x.left == null) return x.right;
if (x.right == null) return x.left;
//x的两个子结点都有元素,此处我们选择小于x的最大的元素
Node t = x;//23
maxMin = x.left;//18,22
while (maxMin.right != null) {
maxMin = maxMin.right;
}
//删除t.left结点最大的元素,并调整n
maxMin.left = deleteMax(t.left);
maxMin.right = t.right;
}
maxMin.n = size(maxMin.left) + size(maxMin.right) + 1;
return maxMin;
}
private Node deleteMax(Node x) {
if (x.right == null) return x.left;
x.right = deleteMax(x.right);
x.n = size(x.left) + size(x.right) + 1;
return x;
}
/*
* 在实现delete之前,依旧还是先明确一下
* delete的要求:
*
* 1.找到目标元素
* 2.找到需要替换的元素并移除
* 3.替换属性
* 用来替换的元素,要满足:比他小的元素中最大的那个/比他大的元素中最小的那个
*
* */
public void delete1(Key key) {
Node ta = get(root, key);
if (ta.left != null) {
//比它小的最大
Node cur = ta.left;
while (cur.right != null) {
cur = cur.right;
}
deleteNode(cur);
ta.key = cur.key;
ta.val = cur.val;
} else if (ta.right != null) {
//比它大的最小
Node cur = ta.right;
while (cur.left != null) {
cur = cur.left;
}
deleteNode(cur);
ta.key = cur.key;
ta.val = cur.val;
} else {
deleteNode(ta);
}
}
private void deleteNode(Node ta) {
Node fa = getFather(ta);
if (fa == null) {
//ta == root
ta.key = null;
ta.val = null;
ta.n -= 1;
} else {
if (fa.left == ta) {
fa.left = null;
} else {
fa.right = null;
}
fa.n -= 1;
}
}
private Node getFather(Node ta) {
Node cur = root;
if (root == ta) return null;
while (cur.left != ta && cur.right != ta) {
int cmp = ta.key.compareTo(cur.key);
if (cmp > 0) {
cur = cur.right;
} else if (cmp < 0) {
cur = cur.left;
}
}
return cur;
}
@Override
public int size() {
return size(root);
}
private int size(Node node) {
if (node == null) {
return 0;
}
return node.n;
}
@Override
public Key min() {
Node cur = root;
while (cur.left != null) {
cur = cur.left;
}
return cur.key;
}
@Override
public Key max() {
return max(root);
}
private Key max(Node cur) {
if (cur.right == null) return cur.key;
return max(cur.right);
}
//floor 与 ceiling 让我再一次意识到,我不懂递归
@Override
public Key floor(Key key) {
Node ta = floor(root, key);
if (ta == null) {
return null;
}
return ta.key;
}
//这种代码,与其是工程上的实现,不若是智慧的结晶,graceful
private Node floor(Node cur, Key key) {
if (cur == null) return null;
int cmp = key.compareTo(cur.key);
if (cmp == 0) return cur;
else if (cmp < 0) {
return floor(cur.left, key);//如果没有left,说明不存在比key小的元素
}else {
//当前元素小于key
Node t = floor(cur.right, key);
if (t == null) {
return cur;
} else {
return t;
}
}
}
@Override
public Key ceiling(Key key) {
Node ta = ceiling(root, key);
if (ta == null) {
return null;
}
return ta.key;
}
private Node ceiling(Node cur, Key key) {
if (cur == null) return null;
int cmp = key.compareTo(cur.key);
if (cmp == 0) return cur;
else if (cmp > 0) {
return floor(cur.right, key);//如果没有right,说明不存在比key大的元素
}else {
Node t = floor(cur.left, key);
if (t == null) {
return cur;
} else {
return t;
}
}
}
//下面的关于floor&ceiling的实现,要求key是表中的元素。更通用的算法应该是
//floor :返回小于等于key的最大的那个元素
//ceiling:返回大于等于key的最小的那个元素
//小于key的最大键:key所对应的node的left的right end
public Key floor1(Key key) {
Node ta = get(root,key);
Node sa;
for (sa = ta.left; sa.right != null; sa = sa.right) {
}
return sa.key;
}
public Key ceiling1(Key key) {
Node ta = get(root,key);
return ceilingRecursion(ta.right,key);
}
//大于key的最小键:key所对应的node的right的left end
private Key ceilingRecursion(Node cur,Key key) {
if (cur.left == null) return cur.key;
return ceilingRecursion(cur.left,key);
}
//在写rank 与 select 方法前,我们先定义
//排名为k 的键 表明树中正好有k个小于它的键
//左子树节点数量=t,t=k则返回该节点,t>k,这在左子树中继续查找,t<k则在右子树中找 k-t-1
@Override
public int rank(Key key) {
return rank(root, key);
}
private int rank(Node x, Key key) {
if (x == null) return 0;
int cmp = key.compareTo(x.key);
if (cmp < 0) {
return rank(x.left, key);
} else if (cmp > 0) {
return size(x.left) + 1 + rank(x.right, key);
} else {
return size(x.left) ;
}
}
@Override
public Key select(int k) {
return select(root, k).key;
}
private Node select(Node x, int k) {
if (x == null) return null;
int t = size(x.left);
if (t > k) {
return select(x.left, k);
} else if (t < k) {
return select(x.right, k-t-1);
} else {
return x;
}
}
@Override
public Iterable<Key> keys() {
Queue<Key> queue = new ListQueue<>();
keys(root, queue);
return queue;
}
private void keys(Node cur,Queue<Key> queue) {
if (cur == null) return;
queue.enqueue(cur.key);
keys(cur.left, queue);
keys(cur.right,queue);
}
public static void main(String[] args) {
SimpleOrderST bstMap = new BSTMap();
bstMap.put(4,"d");
bstMap.put(2,"b");
bstMap.put(6,"f");
bstMap.put(1,"a");
bstMap.put(3,"c");
bstMap.put(5,"e");
bstMap.put(7,"g");
bstMap.put(7,"z");
System.out.println(bstMap.get(5));
bstMap.delete(4);
}
}
Ps:注意上面这段代码的 delete&floor&ceiling&rank&select 都是对递归的极好练习,值得反复实现甚至背诵
其他的没仔细看,再次回顾依然觉得,这里的delete方法,真巧妙…
当你对二叉查找树做第一次测试时,便会很容易的发现,其树的形状,完全取决于输入元素的顺序。这算是一个绝对的缺点,特定输入下,二叉搜索树会退化成链表。O(lgn) 变成 O(n);
相较于无序链表,肉眼可见的快。代码?下一次吧。
我应该把二叉查找树的每个算法分开,再理解实现一次!这将会是23树,红黑树,以及后面图的部分的基础。
20231220 18:54:在无数次尝试之后,我一次又一次的承认,离开了图书馆我是不会学习的,三天6小时,我能完成BSTMap的再度理解吗?能完成2-3树与红黑树吗?承平日久,不记得过去的原动力与绝望了。
上面已经包含了全部的代码,现在对这些进行二次理解,从21年开始转行到现在勉强算三年,一直有一个极大的困惑便是如何学习项目,即使把代码给我,我看了一遍又一遍,对未知的恐惧与不自信依旧存在,直到开始接触cs61b,我暂时先到的最佳实践便是,1.一定要自己实现,2.实现前一定要有那种“枝枝说到叶叶上”版详细的说明。所以下面的结构便是采取:先给出api->每个方法的仔细描述->我的代码实现->书中的代码实现。不要担心时间,在BSTMap上的投入也是在2-3树&图上的投入,这绝对是值得的。
api:
package define;
public interface SimpleOrderST<Key extends Comparable<Key>,Value> {
void put(Key key, Value value);
Value get(Key key);
void delete(Key key);
default boolean contains(Key key) {
return get(key) != null;
}
default boolean isEmpty() {
return size() == 0;
}
int size();
Key min();
Key max();
/**
* 小于等于key的最大键
* @param key
* @return
*/
Key floor(Key key);
/**
* 大于等于key的最小键
* @param key
* @return
*/
Key ceiling(Key key);
int rank(Key key);//小于key的键的数量
Key select(int k);//排名为k 的键
Iterable<Key> keys();
}
数据结构:
package define;
public class BSTMap<Key extends Comparable<Key>, Value> implements SimpleOrderST<Key, Value>{
private Node root;
private class Node {
private Key key;
private Value val;
private Node left,right;//左右子结点。
private int n;//以该节点作为根的子树的节点数量。
public Node (Key key, Value val,int n) {
this.key = key;
this.val = val;
this.n = n;
}
}
@Override
public void put(Key key, Value value) {
}
@Override
public Value get(Key key) {
return null;
}
@Override
public void delete(Key key) {
}
@Override
public int size() {
return 0;
}
@Override
public Key min() {
return null;
}
@Override
public Key max() {
return null;
}
@Override
public Key floor(Key key) {
return null;
}
@Override
public Key ceiling(Key key) {
return null;
}
@Override
public int rank(Key key) {
return 0;
}
@Override
public Key select(int k) {
return null;
}
@Override
public Iterable<Key> keys() {
return null;
}
}
get:
get非常的简单,只需要在树中进行二分查找,没找到就返回null,找到则返回对应value
@Override
public Value get(Key key) {
Node ta = get(root, key);
if (ta == null) {
return null;
} else {
return ta.val;
}
}
private Node get(Node node,Key key) {
if (node == null) return null;
int cmp = key.compareTo(node.key);
if (cmp > 0) {
return get(node.right, key);
} else if (cmp < 0) {
return get(node.left, key);
} else {
return node;
}
}
put:
对put方法的要求便是:
1.如果树中不存在该key则,需要在合适的位置,新增一个node结点
2.如果树中存在该key则,需要将其val替换成我们的key
相比于get方法,put的难点在于如何在合适位置新增一个结点。想一想现实中是如何做的?当我已经进入了下一个结点,如何获取父节点并知道我是父节点的左儿子还是右儿子?
一种直观的解决方式:1.进入当前结点;2.判断当前结点是否是要找的;3.如果不是则在进入下一个结点前先判断是否是null,null这新增并将下一个结点设置为新增的这个。
@Override
public void put(Key key, Value value) {
if (root == null) {
root = new Node(key, value, 1);
} else {
put(root, key, value);
}
}
private void put(Node node, Key key, Value value) {
int cmp = key.compareTo(node.key);
if (cmp == 0) {
node.val = value;
} else if (cmp > 0) {
if (node.right != null) {
put(node.right, key, value);
} else {
node.right = new Node(key, value, 1);
}
} else {
if (node.left != null) {
put(node.left, key, value);
} else {
node.left = new Node(key, value, 1);
}
}
}
在写完这些之后,随即发现,一旦涉及新增还需要修改搜索链路上的每个结点的n值,我们不可能在进入结点的时候就知道这个节点的n值不变呢还是+1,so只能在递归层层向上返回的时候带上n相关的信息,那么我们必须修改辅助方法的返回值,让其返回n相关的信息。
@Override
public void put(Key key, Value value) {
if (root == null) {
root = new Node(key, value, 1);
} else {
put(root, key, value);
}
}
private int put(Node node, Key key, Value value) {
int cmp = key.compareTo(node.key);
if (cmp == 0) {
node.val = value;
} else if (cmp > 0) {
if (node.right != null) {
node.n = put(node.right, key, value);
} else {
node.right = new Node(key, value, 1);
node.n += 1;
}
} else {
if (node.left != null) {
node.n = put(node.left, key, value);
} else {
node.left = new Node(key, value, 1);
node.n += 1;
}
}
return node.n;
}
经过一番努力,我们终于得到了完完全全属于自己的put方法,一个拥有知识产权的put方法。这是值得祝贺的事情,不过那一堆的if else看着如此的别扭,那种是否为null的判断一下子就让人警觉起来,那个目前我还不懂的概念蹦出来了:cs61b中强调的「arms-length base case」,Josh Hug教授强调要避免的null判断出现在我的代码中了。可以仔细想想还能怎么优化?下面的优化是我在已经见过书中的代码并理解了的情况下写出来的,只有自己想出来的才是真真自己的,递归,层层向下深入,触底再层层向上返回,我们需要返回给上一层的信息来自方法的返回值。也仅有返回值可以传递给上一层,递归其实不仅建立了a-b的联系,也建立了b-a的联系。so 答案是什么呢?
书中的答案则是,可以在返回子节点,这样在每次层层深入时我就告诉当前环境,你的子节点就是待会儿函数的return,而每一层的函数呢,则只需要判断当前结点是否为null,不是则计算n && 返回自己,是就新增。一个看着很清爽像数学公式一样美丽的东西诞生了
@Override
public void put(Key key, Value value) {
root = put(root, key, value);
}
private Node put(Node node, Key key, Value value) {
if (node == null) {
return new Node(key, value, 1);
}
int cmp = key.compareTo(node.key);
if (cmp > 0) {
node.right = put(node.right, key, value);
} else if (cmp < 0) {
node.left = put(node.left, key, value);
} else {
node.val = value;
}
node.n = size(node.left) + size(node.right) + 1;
return node;
}
至此,put方法算是结束了
delete:
现在已经8点了,老实说我到现在都没有完全的信心与决心去完成delete方法,可问题终归要去解决。
我先来一段书中关于delete方法的介绍:“二叉查找树中最难实现的方法就是delete方法”。在delete的最终实现前,我们先来一点热身运动,deleteMin & deleteMax。
对于deleteMin:一路向左,直到遇到一个结点,其左儿子=null,此时将指向该结点的链接修改为指向该结点的右儿子。deleteMax类似。
关于删除min/max的代码应该如何实现呢,首先我们明确,需要修改树的结构,可以参考put方法的递归实现,返回每一个链接修改之后的结点。
private Node deleteMin(Node node) {
if (node == null) return null;
Node original = node.left;
node.left = deleteMin(node.left);
node.n = size(node.left) + size(node.right) + 1;
if (original == null) {
return node.right;
}
return node;
}
public void deleteMax() {
deleteMax(root);
}
private Node deleteMax(Node node) {
if (node == null) return null;
Node original = node.right;
node.right = deleteMax(node.right);
node.n = size(node.left) + size(node.right) + 1;
if (original == null) {
return node.left;
}
return node;
}
那个original的存在,总是让代码看着如此的不舒服,尤其是对他还有一个==null的判断,下面我们来看一看书中关于这一段的抽象。
public void deleteMin() {
deleteMin(root);
}
private Node deleteMin(Node node) {
if (node.left == null) return node.right;
node.left = deleteMin(node.left);
node.n = size(node.left) + size(node.right) + 1;
return node;
}
public void deleteMax() {
deleteMax(root);
}
private Node deleteMax(Node node) {
if (node.right == null) return node.left;
node.right = deleteMax(node.right);
node.n = size(node.left) + size(node.right) + 1;
return node;
}
以min为例,当前环境函数的返回值是上一个环境(上一个结点)的左儿子,而根据描述,删除最小即将最小结点上一个结点的左儿子(原本是最小结点)设置为最小结点的右儿子,这是一个三层关系。简单描述:当前结点是否是最小结点,如果是则返回当前结点的右儿子给当前结点的父节点当左儿子,如果不是则当前结点的左儿子去下一个结点里面找。与模范相比,我不得不再一次问自己,真的懂了我要干什么吗?
我们必须在自己的实现与最佳实践中寻找并理解差距,以不断的缩小这种差距。为什么有时候会产生代码为何如此难以看懂的感觉,如此多有细微差异大体相同的代码?可以多问问自己对事情的抽象真的已经是最佳的了吗。
关于删除,我们可以用类似的方法删除任意一个只有一个子结点的结点,即将指向它的链接指向其存在的子节点。如果该结点存在两个子结点又该如何进行删除呢?删除之后我们存在两颗子树,可空出来的链接只有一个。答案便是用后继结点来替换将要被删除的结点。后继结点其实就是被删除结点的邻居,左子树的最大值/右子树的最小值。书中以右子树的最小结点为例,此处就以左子树的最大结点为例。
1.找到我们要删除的结点
2.将其设置为max(left)
3.删除左子树的最大结点,同时继承左子树
4.继承原来的右子树
代码似乎呼之欲出:
@Override
public void delete(Key key) {
delete(root, key);
}
private Node delete(Node node, Key key) {
if (node == null) return null;
int cmp = key.compareTo(node.key);
if (cmp > 0) {
node.right = delete(node.right, key);
} else if (cmp < 0) {
node.left = delete(node.left, key);
} else {
//当前结点就是要删除的结点
if (node.left == null) return node.right;
if (node.right == null) return node.left;
//走到这里来了,说明其有两颗子树
Node t = node;
//1.将其设置为左子树的最大结点
node = max(node.left);
//2.继承并删除左子树
node.left = deleteMax(t.left);//注意是将当前结点的左子树设置为之前结点的左子树,并删除之前结点左子树的最大值
//3.继承右子树
node.right = t.right;
}
node.n = size(node.left) + size(node.right) + 1;
return node;
}
这是书中的解决办法,精巧美妙。我自己之前的实现这是反复的去找结点,找父节点,虽然糟糕,倒也能实现功能。
public void delete1(Key key) {
Node ta = get(root, key);
if (ta.left != null) {
//比它小的最大
Node cur = ta.left;
while (cur.right != null) {
cur = cur.right;
}
deleteNode(cur);
ta.key = cur.key;
ta.val = cur.val;
} else if (ta.right != null) {
//比它大的最小
Node cur = ta.right;
while (cur.left != null) {
cur = cur.left;
}
deleteNode(cur);
ta.key = cur.key;
ta.val = cur.val;
} else {
deleteNode(ta);
}
}
private void deleteNode(Node ta) {
Node fa = getFather(ta);
if (fa == null) {
//ta == root
ta.key = null;
ta.val = null;
ta.n -= 1;
} else {
if (fa.left == ta) {
fa.left = null;
} else {
fa.right = null;
}
fa.n -= 1;
}
}
private Node getFather(Node ta) {
Node cur = root;
if (root == ta) return null;
while (cur.left != ta && cur.right != ta) {
int cmp = ta.key.compareTo(cur.key);
if (cmp > 0) {
cur = cur.right;
} else if (cmp < 0) {
cur = cur.left;
}
}
return cur;
}
下面的这种实现很难说有什么天大的错误,为什么代码的复杂度上去了呢?我觉得更多的是对解决方案的抽象不同,再进一步则是对我们将要做的事情的理解限制了代码的最终实现。回到cs61b开篇的那句话:“软件很少被物理条件限制,几乎是一个纯粹的创造性活动,最大的限制是对我们所构建的东西的理解。”
size:
size方法,用来统计当前树有多少个节点的,而我们对node里面n的定义则是返回以该结点为root的子树节点数量。故size只需要返回root节点的n即可。
@Override
public int size() {
return size(root);
}
private int size(Node node) {
if (node == null) {
return 0;
}
return node.n;
}
min:
min方法的目的是找到这棵树最小的节点,根据BST的定义,其存在于树的最左端,left到底。
比较容易实现,可以递归,也可以循环。
@Override
public Key min() {
if (root == null) return null;
Node cur = root;
for (;cur.left != null; cur = cur.left);
return cur.key;
}
max:
max方法是为了返回这棵树的最大的节点,其存在于树的最右端,right到底。
既然left走了循环,max就来个递归呗。
@Override
public Key max() {
if (root == null) return null;
Node ta = max(root);
return ta.key;
}
private Node max(Node node) {
if (node.right == null) {
return node;
} else {
return max(node.right);
}
}
floor:
再处理完delete之后,floor与ceiling的实现就变得比较简单了,floor:小于key的最大键;ceiling:大于key的最小键,不就是我们在删除中需要处理的左子树的最大值与右子树的最小值。
额,即使是简单的功能也不能掉以轻心,这里又犯了一个错误,我们不应该假设key一定存在,
1.key存在,返回key
2.key比当前所有节点都小,返回null
3.key比某个节点大,而该结点又没有右子树的时候,该结点就是我们找的
@Override
public Key floor(Key key) {
Node ta = floor(root, key);
if (ta == null) {
return null;
}
return ta.key;
}
private Node floor(Node node, Key key) {
if (node == null) return null;
int cmp = key.compareTo(node.key);
if (cmp > 0) {
Node t = floor(node.right, key);
if (t == null) {
return node;
}
return t;
} else if (cmp < 0) {
return floor(node.left, key);
} else {
return node;
}
}
ceiling:
略
rank:
rank与select 又是比较麻烦的一组,这里涉及到如何在一棵搜索二叉树中定义序列,书中给的定义便是要想找到排名为k的结点,即表明树中有k个结点小于其,故其左子树结点数量应该为k。其右子树rank = 左子树+1;
@Override
public int rank(Key key) {
return rank(root, key);
}
private int rank(Node node, Key key) {
if (node == null) return 0;
int cmp = key.compareTo(node.key);
if (cmp > 0) {
return size(node.left) + 1 + rank(node.right, key);
} else if (cmp < 0) {
return rank(node.left, key);
} else {
return size(node.left);
}
}
select:
@Override
public Key select(int k) {
Node ta = select(root, k);
if (ta == null) {
return null;
}
return ta.key;
}
private Node select(Node node, int k) {
if (node == null) return null;
int l = size(node.left);
if (k < l) {
return select(node.left, k);
} else if (k > l) {
return select(node.right, k - l - 1);
} else {
return node;
}
}
keys:
keys的实现 skip。
继上周写下BSTMap之后,总算在花了不是那么全神贯注的三个晚上,再次过了一遍,值得吗?可生活哪有这么多值不值得,今晚走神的严重一点,可前两晚上对递归的练习是实实在在的,真真切切的。也许将来不会记得这些,可过去的时间至少让你觉得没那么焦虑,很放松,生活似乎有点意义了。周末,努力干掉2-3树,红黑树,相信在BSTMap上的耗费,会在这些上面事半功倍!生活太难,那就专注当下吧,期望与公交上的学生同行!
3.2-3树及其红黑树实现
14:45 二叉查找树的相关代码,写完感觉人很累,甚至有种完全不想动的感觉了,过去无数次发生在我身上的回忆又回来了,一种无法静心的烦躁,可能源于对前面代码的敷衍式学习,因为身体明显知道自己敷衍了,故虽有时间上的付出,却无任何实际的获得感。不想再学习任何与树有关的结构了。skip this,下周再处理。
上周的一个skip,就到了这周的周天,现在是10:18。
前面我们学习的二叉搜索树,现在开始进阶2-3树&红黑树,在介绍之前,可以先看一下cs61b中的关于b树(做人要有b树🤣)的介绍,核心:树的高度不变&允许叶子结点存多个值&限制叶子结点能保存的个数。
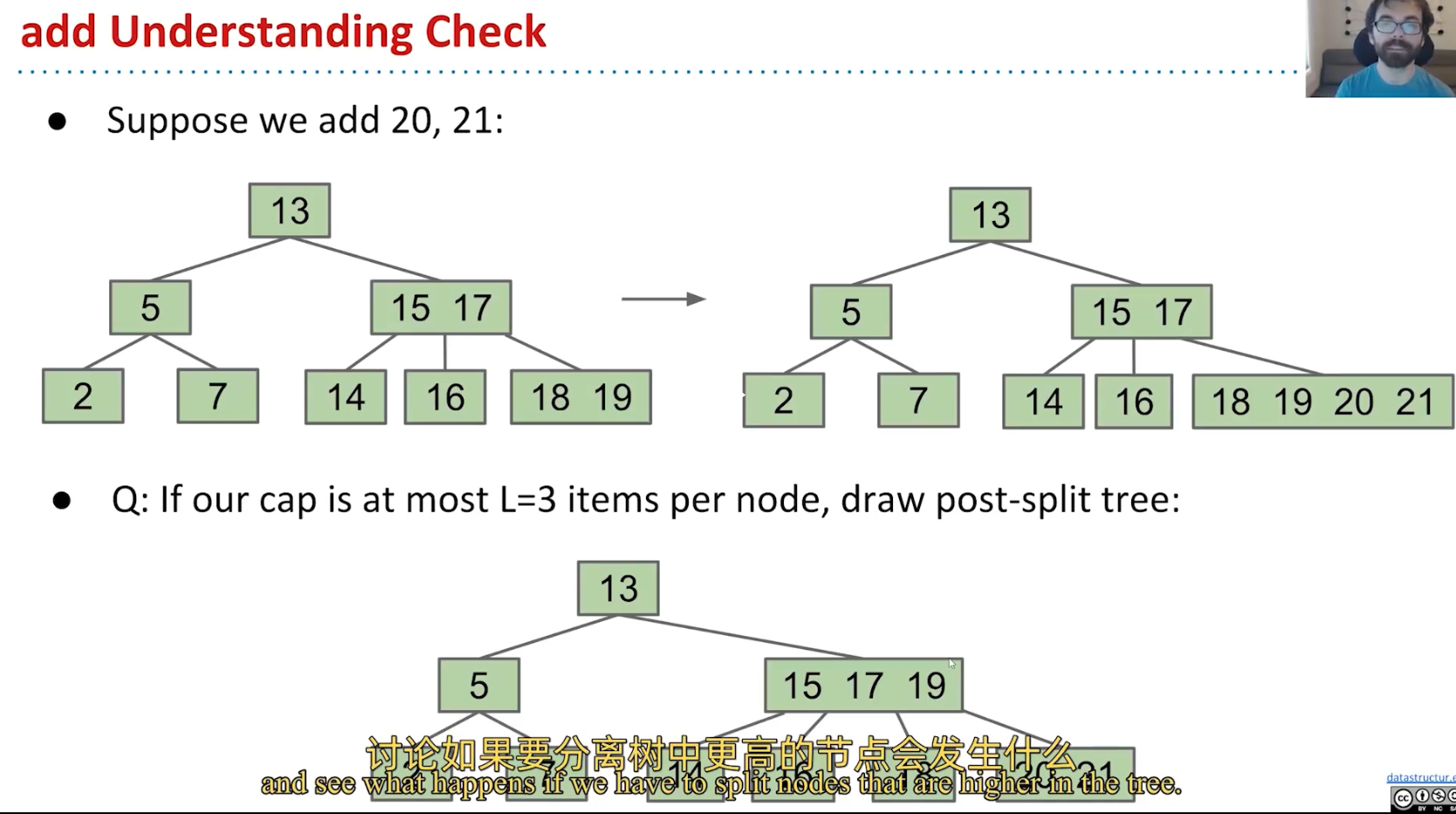
只要对二叉搜索树稍微进行插入,便会发现,最终树的形状完全取决于插入的顺序…,一般我们无法控制插入的顺序,所以对最坏情况的分析是唯一能提供性能保证的方法。
Worst case BST hight is O(N);
Height,Depth,Performance:
Depth:distance of node to root;
Height: deepest leaf; worst runtime to find a node;
Average depth:(node-num*depth)/sum(node);
Good news:random operation BST ~ O(log(N))
Bad news:neraly can`t operate random; data comes in over time;
B-tree:avoiding imbalance;
1.hight no change; – leaf become leaves;
2.leaf nodes avoid too juice;– limit ,over limit give one to parent(left middle)
二叉查找树的结点,称之为标准的2-结点,保存一个k-v,带两个儿子。
3-结点则是保存2个k-v,带3个儿子。
2-3树,要么是空树,要么由2-结点/3-结点组成。
一颗完美平衡的2-3树,其所有空链接到root结点的距离都是相同的。
查找的流程就不再详细描述,重点留意插入过程,关于插入的详细文字描述,算法树中写的很不错了,重点在于我们在插入过程中,所有的局部变换都没有破坏树的平衡性,即使根节点的变换也只是让树的高度+1,树依旧是平衡的,所有的空链接到根节点的深度是一致的。局部变换,并不会影响树的全局有序与平衡。
二叉查找树是向下生长,2-3树则是向上生长。
2-3树的查找与插入,O(lgN)
对数性质,使得10亿左右的键一般情况下高度在19~30之间,则是十分恐怖的性能。
让人感到恐惧的红黑树,其实是2-3树比较简洁的代码实现,囧…
关于红黑树的左旋,右旋,颜色反转这些及具体的在put方法中遇到的每一种情况的处理方式及对这些方式的最终抽象,书中已经描述的非常细节了,此处如果我要去描述的话,只能把那些略显繁琐又充满细节的描述原封不动的搬过来,so此处略去。
我们先从一个大的范围上理解红黑树。红黑树是什么?红黑树应该是2-3树的一种具体实现,类似于用数组去实现堆结构。本质是用二叉查找树+链接颜色 来表示2-3树,对于get等不改变树结构的方法,将其当作二叉搜索树处理即可,而对于put&delete等改变树结构的方法,在口述阶段我们需要用2-3树的逻辑来描述,然后再考虑将其翻译成红黑树的代码实现。
本次介绍的红黑树实现,更应该称之为:Left-Leaning Red Black Binary Search Tree (LLRB)
每一颗红黑树,我们将红色链接打平都是一颗2-3树,并且二者之间存在绝对的一一对应关系。
关于红黑树就不再一个一个方法拆解并实现了,而是给一个笼统的最终版本。
20231224-18:31 很惭愧,没能理解删除。
20240101 13:35 还是没能理解红黑树的删除操作,在昨晚烧了一整天之后(是要红红火火的意思吗),现在稍放松,却又困顿起来了。
左倾红黑树:二叉搜索树实现的2-3树,我们操作的一个核心要点便是要保持平衡,这也是2-3树最吸引人的特点。
删除时,如果我们要删除的结点时3结点,直接删除就可以了,可如果要删除的结点是2结点,
1.兄弟结点是3结点,通过旋转,弄一个过来
2.兄弟结点是2结点,左右儿子都变成红色,组装成一个大结点
在递归深入的时候,需要不停的将各种结点进行变换,返回时又需要处理我们临时变换后的结点。
package define;
public class RedBlackTree<Key extends Comparable<Key>,Value> implements SimpleOrderST<Key, Value>{
Node root;
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node {
Key key;
Value val;
Node left, right;
int n;
boolean color;
Node(Key key, Value val, int n, boolean color) {
this.key = key;
this.val = val;
this.n = n;
this.color = color;
}
}
private boolean isRed(Node x) {
if (x == null) return false;
return x.color == RED;
}
private Node rotateLeft(Node h) {
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = h.color;
h.color = RED;
x.n = h.n;
h.n = size(h.left) + size(h.right) + 1;
return x;
}
private Node rotateRight(Node h) {
Node x = h.left;
h.left = x.right;
x.right = h;
x.color = h.color;
h.color = RED;
x.n = h.n;
h.n = size(h.left) + size(h.right) + 1;
return x;
}
private void flipColors(Node h) {
h.left.color = BLACK;
h.right.color = BLACK;
h.color = RED;
}
private void flipColorsForDelete(Node h) {
h.left.color = RED;
h.right.color = RED;
h.color = BLACK;
}
@Override
public void put(Key key, Value value) {
root = put(root, key, value);
root.color = BLACK;
}
private Node put(Node node, Key key, Value value) {
if (node == null) {
return new Node(key, value, 1, RED);
}
int cmp = key.compareTo(node.key);
if (cmp > 0) {
node.right = put(node.right, key, value);
} else if (cmp < 0) {
node.left = put(node.left, key, value);
} else {
node.val = value;
}
if (isRed(node.left) && isRed(node.right)) flipColors(node);
if (isRed(node.left) && isRed(node.left.left)) rotateRight(node);
if (!isRed(node.left) && isRed(node.right)) rotateLeft(node);
node.n = size(node.left) + size(node.right) + 1;
return node;
}
@Override
public Value get(Key key) {
Node ta = get(root, key);
if (ta == null) {
return null;
} else {
return ta.val;
}
}
private Node get(Node node, Key key) {
if (node == null) return null;
int cmp = key.compareTo(node.key);
if (cmp > 0) {
return get(node.right, key);
} else if (cmp < 0) {
return get(node.left, key);
} else {
return node;
}
}
@Override
public void delete(Key key) {
if (!isRed(root.left) && !isRed(root.right)) {
root.color = RED;
}
root = delete(root, key);
if (!isEmpty()) root.color = BLACK;
}
private Node delete(Node h, Key key) {
int cmp = key.compareTo(h.key);
if (cmp < 0) {
//2结点参照deletemin
if (!isRed(h.left) && !isRed(h.left.left)) {
h = moveRedLeft(h);
}
h.left = delete(h.left, key);
} else {
if (isRed(h.left)) {
//三结点中偏大的那一个
h = rotateRight(h);
}
if (cmp == 0 && h.right == null) {
//在经过变换后的二叉搜索树形态,当前结点是我们要删除的结点,且没有儿子,叶子结点,直接删除
return null;
}
if (!isRed(h.right) && !isRed(h.right.left)) {
//2结点参照deletemax
h = moveRedRight(h);
}
if (cmp == 0) {
Node ta = get(h.right, min(h.right).key);
h.key = ta.key;
h.val = ta.val;
h.right = deleteMin(h.right);
} else {
h.right = delete(h.right, key);
}
}
return balance(h);
}
public void deleteMin() {
if (!isRed(root.left) && !isRed(root.right)) {
root.color = RED;
}
root = deleteMin(root);
if (!isEmpty()) root.color = BLACK;
}
private Node deleteMin(Node h) {
if (h.left == null) {
return null;
}
if (!isRed(h.left) && !isRed(h.left.left)) {
//是一个2结点,需要处理
h = moveRedLeft(h);
}
h.left = deleteMin(h.left);
return balance(h);
}
private Node balance(Node h) {
if (isRed(h.right)) {
h = rotateLeft(h);
}
if (isRed(h.left) && isRed(h.right)) flipColors(h);
if (isRed(h.left) && isRed(h.left.left)) rotateRight(h);
if (!isRed(h.left) && isRed(h.right)) rotateLeft(h);
h.n = size(h.left) + size(h.right) + 1;
return h;
}
private Node moveRedLeft(Node h) {
flipColorsForDelete(h);
if (isRed(h.right.left)) {
h.right = rotateRight(h.right);
h = rotateLeft(h);
}
return h;
}
public void deleteMax() {
if (!isRed(root.left) && !isRed(root.right)) {
root.color = RED;
}
root = deleteMax(root);
if (!isEmpty()) root.color = BLACK;
}
private Node deleteMax(Node h) {
if (isRed(h.left)) {
h = rotateRight(h);
}
if (h.right == null) {
return null;
}
if (!isRed(h.right) && !isRed(h.right.left)) {
h = moveRedRight(h);
}
h.right = deleteMax(h.right);
return balance(h);
}
private Node moveRedRight(Node h) {
flipColorsForDelete(h);
if (!isRed(h.left.left)) {
h = rotateRight(h);
}
return h;
}
@Override
public int size() {
return size(root);
}
private int size(Node node) {
if (node == null) {
return 0;
}
return node.n;
}
@Override
public Key min() {
Node ta = min(root);
if (ta == null) {
return null;
}
return ta.key;
}
private Node min(Node h) {
if (h == null) return null;
return min(h.left);
}
@Override
public Key max() {
return null;
}
@Override
public Key floor(Key key) {
return null;
}
@Override
public Key ceiling(Key key) {
return null;
}
@Override
public int rank(Key key) {
return 0;
}
@Override
public Key select(int k) {
return null;
}
@Override
public Iterable<Key> keys() {
return null;
}
}
对红黑树,似乎有了一个简单的模糊的,不那么精确的概念,与代码实现,但代码中依旧存在诸多不太明白的地方,有待进一步的探索与掌握。it·s hard but worth。
20250721 再次复习时,我选择放弃,根本没有概念…,我需要再看一次书或者cs61b中的视频讲解…(😣)
4.散列表
这是一个极其通用的数据结构,在我自21年10月入行至今,所待的两个项目,除了arraylist外,hashmap 便是使用最多的了。散列表是算法在时间和空间上作出权衡的经典例子。
使用散列的查找算法分成两步:
1.使用散列函数将被查找的键转换成数组的一个索引。
2.处理碰撞冲突。
在本节中将会介绍两种处理冲突的方法:拉链法&线性探测法
散列函数:其主要目的便是 将键转换成数组的索引。
介绍一些通用的散列方法:
- 正整数:除留余数法,k%m。m最好为素数。
- 浮点数:对于0~1之间的实数,k*m再四舍五入,缺陷在于低位几乎没用处。better:键转换成二进制然后再除留余法。
- 字符串:hash = (R*hash+s.charAt(i))%m
有时糟糕的散列函数也是性能问题的罪魁祸首,如果散列计算比较耗时,可以使用缓存,即使用一个变量来保存对象的hashcode,只在第一次使用的时候进行计算。
基于拉链法的散列表
come on baby,i am coming…
数组下标说对应的值,指向一个链表,链表的每个结点都存储了散列值相同的k-v键值对。
Show me code
package define;
public class SeparateChainingHashST <Key, Value> implements SimpleST<Key, Value> {
private int n;//键值对总数
private int m;//散列表大小
private SequentialSearchST<Key, Value>[] st;
public SeparateChainingHashST() {
this(997);
}
public SeparateChainingHashST(int m) {
this.m = m;
st = (SequentialSearchST<Key, Value>[])new SequentialSearchST[m];
for (int i = 0; i < m; i++) {
st[i] = new SequentialSearchST<>();
}
}
private int hash(Key key) {
return (key.hashCode() & 0x7fffffff) % m;
}
@Override
public void put(Key key, Value value) {
st[hash(key)].put(key, value);
n++;
}
@Override
public Value get(Key key) {
return st[hash(key)].get(key);
}
@Override
public void delete(Key key) {
st[hash(key)].delete(key);
n--;
}
@Override
public int size() {
return n;
}
<
@Override
public Iterable<Key> keys() {
return null;
}
}
这是如此的简单与优雅,几乎不怎么耗费大脑,却得到了恐怖的性能提升,这就是思想的力量!
基于拉链法的散列表对碰撞冲突的解决办法便是将拥有相同hash值的k-v对保存在一个链表/数组内。还有一类处理方式便是在大小m的数组中储存n对k-v,其中m>n,利用多余的空位解决碰撞冲突,采用这种策略的方法统一称为:开放地址散列表。
基于线性探测法的散列表
开放地址散列表中最简单的方法便是线性探测法。
当发生碰撞时,我们直接将索引+1,检查下一个位置
- 命中则更新
- 未命中,位置为null,则放入
- 未命中,位置存放了其他key,继续查找
重复上述步骤,直到找到该元素/null为止。
探测:检查数组位置是否含有被查找的键。
package define;
import java.util.Arrays;
public class LinearProbingHashST<Key, Value> implements SimpleST<Key, Value> {
private int n;//k-v 对的数量
private int m = 16;//线性探测表的大小
private Key[] keys;
private Value[] values;
public LinearProbingHashST(int m) {
keys = (Key[]) new Object[m];
values = (Value[]) new Object[m];
this.m = m;
}
public LinearProbingHashST() {
keys = (Key[]) new Object[m];
values = (Value[]) new Object[m];
}
private int hash(Key key) {
return (key.hashCode() & 0x7fffffff) % m;
}
/**
* 这是一个十足的负面例子,这种resize的实现是绝对的错误
* 因为随着m的变化,hash的返回值也是不同的
* @param m
*/
private void resize_error(int m) {
Key[] nk = (Key[]) new Object[m];
Value[] nv = (Value[]) new Object[m];
System.arraycopy(keys,0, nk,0,m);
System.arraycopy(values,0, nv,0,m);
keys = nk;
values = nv;
this.m = m;
}
private void resize(int m) {
LinearProbingHashST<Key, Value> nt = new LinearProbingHashST(m);
for (int i = 0; i < this.m; i++) {
nt.put(keys[i], values[i]);
}
this.keys = nt.keys;
this.values = nt.values;
this.m = m;
}
@Override
public void put(Key key, Value value) {
if (n > m/2) resize(2*m);
int i = hash(key);
for (;keys[i] != null; i = (i + 1) % m) {
if (keys[i].equals(key)) {
values[i] = value;
return;
}
}
keys[i] = key;
values[i] = value;
n++;
}
@Override
public Value get(Key key) {
int i = hash(key);
for (;keys[i] != null; i = (i + 1) % m){
if (keys[i].equals(key)) {
return values[i];
}
}
return null;
}
/**
* 删除操作会麻烦一点点,因为不能直接将key所对应的索引设置为null,因为null表示键簇的结束,会导致后面的key无法被找到
* 1.找到目标元素,并将其置为null
* 2.将目标元素直到下一个null为止的中间所有元素,设置为null,并重新放入table
*
* @param key
*/
@Override
public void delete(Key key) {
if (!contains(key)) return;
int i = hash(key);
while (!key.equals(keys[i])) {
i = (i + 1) % m;
}
keys[i] = null;
values[i] = null;
i = (i + 1) % m;
while (keys[i] != null) {
Key mk = keys[i];
Value mv = values[i];
keys[i] = null;
values[i] = null;
n--;
put(mk, mv);
}
n--;
if (n > 0 && n == m/8) resize(m/2);
}
@Override
public int size() {
return n;
}
@Override
public Iterable<Key> keys() {
return Arrays.asList(keys);
}
}
n/m : 表示散列表的使用率,对于拉链法的散列表,其表示每条链表的平均长度。而对于线性探测表示的链表则其不能>=1,一但等于1,未命中的查找将会导致无限循环。为了保证性能,使用率在1/8 ~ 1/2之间是比较合适的。
在线性探测的散列表中,键簇大小会比较明显的影响查找/插入的成本,书中有对此更加专业的数学分析,此处我这里,着实能力欠缺,我所愿意付出的成本是远远不足以完成这些分析的。so skip。
散列表有着优秀的性能,使得常数级别的查找与插入变成可能,那么 古尔丹,缺点是什么呢?
- 每一类型的键,需要优秀的散列函数。性能的保证来自于散列函数的质量。
- 有序,基本与散列绝缘了。
5.符号表应用
我们用索引来描述,一个键与多个值关联的符号表。在map的val中放入一个队列/列表,一个索引便诞生了。
反向索引,便是键与值的互换。
example:
正向:电影&一系列演员
反向:演员&一系列电影
对照索引:每个单词在书中出现的所有位置。
符号表与稀疏向量
这种应用虽然简单,但非常重要,不愿意挖掘其中省时省力的潜力的程序员解决实际问题能力的潜力也必然是有限的,能够将运行速度提升几十亿倍的程序员用于面对看似无法解决的问题。