图

终于来到最后两章了，没有那么多的意义可言，行动！还是行动！前进，继续前进！
在学习之前，不要把图想的非常复杂，他确实是一个相对小的自成一体的领域，在挑战过二叉搜索树，对递归，循环等有了一定练习之后，图不再是一个让人仰望难以攀登的高峰，摸一摸山脚是肯定可以做到的。二叉树算是特殊的图，图比二叉树所描述的更通用，也更广泛。在对特例进行了研究后退回到更低一级的抽象时不应该感到恐惧，更应是一种处处都感到熟悉，曾经来过的感觉。
在这一章的学习中，结构还是基本基于《算法》的安排，先给出图在数学中的一些定义，再给出通用的图数据结构，最后则是完全按照书中安排从无向图、有向图、一步步走到加权图、加权有向图。
20240103-18：56：感冒很痛苦，鼻塞了很久。
在深入图及相关的算法之前，非常有必要介绍一点离散数学中的图论：

图论

对一门严肃的知识，进行游龙戏水般的探索，是否是一种浪费时间呢？对于21年花了一个多月时间简单的过了离散数学随即便忘的一点不剩的我，我倾向于肯定的回答。
图：点集合+边集合+边集合到点集合的函数。

V = ['A', 'B', 'C']
E = ['e1', 'e2', 'e3']
f = {
    'e1': ('A', 'B'),
    'e2': ('B', 'C'),
    'e3': ('A', 'C')
}

邻接点：同一条边上的两个结点。
孤立结点：不与任何结点向领接的结点。
零图：仅由孤立结点构成的图。
平凡图：仅由一个孤立结点构成。
邻接边：同一个结点上的两条边。
自回路/环：关联于同一结点的一条边。环的方向是没有意义的。
结点度数：结点关联的边的数量。
结点度数的总和=边数*2.由此可以推出：每一个图中，度数为奇数的结点个数必然是偶数个。
入度/出度：有向图中的。
简单图：不含有平行边&环的图。
补图：
同构：
路：
迹：路中边均不同
通路：路中所有结点均不同
连通图：图只有一个连通分支
点割集：删除其中所有结点后得到的子图不再是连通图，但删除其任意真子集，还是连通图。
边割集：同上
割点：该点构成点割集
割边：同上
关于图论还有许多的定义，不过完成比完美更重要…

无向图

最简单的图定义：顶点 & 将顶点相连的边 所组成的东西。与树的定义相比少了：两点之间只有唯一的一条路径的限制。
边依附于顶点
顶点的度数
子图：边的子集
路径
简单路径
环
简单环
连通图：任意顶点都存在一条路径到达另一任意顶点。连通图可以一把提起来，非连通图则是由多个连通分量组成。
密度
无向图的抽象api：

package define;

public interface IGraph {
  
    int V();

    int E();

    void addEdge(int v, int w);

    Iterable<Integer> adj(int v);

}

抽象类：

package define;

public abstract class AbstructUndirectedGraph implements IGraph {

}

实现：
一般有如下三种方式：
1.邻接矩阵，用一个v*v的布尔矩阵，但点数太多，及其耗费时间。
2.边的数组，用一个类表示一条边，在用边的数组表示图，adj需要遍历所有边。
3.邻接表数组，以顶点为索引的数组，数组中存放该点所有的邻接点。（数组的索引表示点，内容为与之相邻的点的list（下例中的bag））
书中采用第三种方式，so 本文亦如此了。原因？在进行深入之前，还是先依葫芦画瓢。

package define;

import define.impl.LinkBag;
import edu.princeton.cs.algs4.In;

public class Graph extends AbstructUndirectedGraph{

    private final int V;//多少个点
    private int E;
    private Bag<Integer>[] adj;

    public Graph(int V) {
        this.V = V;
        this.E = 0;
        this.adj = (Bag<Integer>[]) new Bag[V];
        for (int v = 0; v  < V; v++) {
            this.adj[v] = new LinkBag<>();
        }
    }

    public Graph(In in) {
        this(in.readInt());
        int E = in.readInt();
        for (int i = 0; i < E; i++) {
            int v = in.readInt();
            int w = in.readInt();
            this.addEdge(v, w);
        }
    }

    @Override
    public int V() {
        return this.V;
    }

    @Override
    public int E() {
        return this.E;
    }

    @Override
    public void addEdge(int v, int w) {
        adj[v].add(w);
        adj[w].add(v);
        E++;
    }

    @Override
    public Iterable<Integer> adj(int v) {
        return adj[v];
    }
}

在进行了一些概念与数据结构的定义之后，下面准备开始图的相关算法。
图的许多性质与路径有关，一个通用的抽象便是，沿着边从一个顶点到另一个顶点。

深度优先搜索

在对递归有了一定程度的了解后，深度优先算法应该是信手拈来。

1. 从一个点开始，选择一个没有遍历过的点。
2. 每遍历一个点就打上标记。
3. 如果点已经遍历过了就退回到上一个点。
4. 如果上一个点的所有相邻点都遍历过了，就退回到上一个点。

api：

package algorithm.api;

public interface ISearch {
    
    boolean marked(int v);
    
    int count();
}

实现：

package algorithm;

import define.Graph;

public class DepthFristSearch {
    private boolean[] marked;
    private int count;

    public DepthFristSearch(Graph G, int s) {
        marked = new boolean[G.V()];
    }

    private void dfs(Graph G, int v) {
        marked[v] = true;
        count++;
        for (int w : G.adj(v)) {
            if (!marked[w]) dfs(G, w);
        }
    }

    public boolean marked(int w) {
        return marked[w];
    }
    
    public int count() {
        return count;
    }
}

搜索一幅图，只需要一个递归方法遍历所有顶点：

1. 访问过的点打上标记。
2. 递归访问所有没有被标记过点。

无向图中的深度优先算法，每条边都会被访问两次，a到b，这是第一次，b到a这是第二次（a此时已被标记）。
深度优先算法，可以处理：

1. 连通性：给定的两个点之间是否是连通的？图存在多少个连通子图？
2. 单点路径：在给定的一幅图，两个顶点之间是否存在一条路径？

接下来介绍，深度优先算法中的路径查找问题，需要注意的是这里面关于路径的解决技巧会用在后面诸多更加复杂，更加强大的算法中。
api：

package algorithm.api;

public interface IPaths {

    /** 是否存在s到v的路径 */
    boolean hasPathTo(int v);

    /** s到v的路径，如果不存在就返回null */
    Iterable<Integer> pathTo(int v);
}

实现：

package algorithm;

import algorithm.api.IPaths;
import define.Graph;
import define.Stack;
import define.impl.ListStack;

public class DepthFristPaths implements IPaths {
    
    private boolean[] marked;
    
    private int[] edgeTo;
    
    private final int s;
    
    public DepthFristPaths(Graph g, int s) {
        marked = new boolean[g.V()];
        edgeTo = new int[g.V()];
        this.s = s;
        dfs(g, s);
    }
    
    private void dfs(Graph g, int v) {
        marked[v] = true;
        for (int w : g.adj(v)) {
            if (!marked[w]) {
                edgeTo[w] = v;
                dfs(g, w);
            }
        }
    }
    
    @Override
    public boolean hasPathTo(int v) {
        return marked[v];
    }

    @Override
    public Iterable<Integer> pathTo(int v) {
        if (!hasPathTo(v)) return null;
        Stack<Integer> path = new ListStack<>();
        for (int x = v; x != s; x = edgeTo[x]) {
            path.push(x);
        }
        path.push(s);
        return path;
    }
}

对于edgeTo数组而言，里面的边构造出了一棵以s作为root的二叉树。

广度优先搜索

深度优先算法，解决了是否存在连通/路径的问题，倘若要找到最短的路径，则需要广度优先算法。
深度优先搜索在，这个问题上没有什么作为，因为其遍历整个图的顺序与找出最短路径的目标没有任何联系。
如果说深度优先搜索是一个人在走迷宫，那么广度优先搜索则是一群人在走迷宫。
广度优先搜索的基本思想便是：

1. 使用一个队列来保存，已被标记但其领接表还未被检查过的顶点。
2. 取队列中下一个顶点v并标记。
3. 将所有与v相邻并未被标记的顶点加入队列。

深度优先，隐式的使用了一个堆（递归），广度则是现式的使用了一个队列。
api 同深度搜索优先一致
实现：

package algorithm;

import algorithm.api.IPaths;
import define.Graph;
import define.Queue;
import define.Stack;
import define.impl.ListQueue;
import define.impl.ListStack;

public class BreadthFristPaths implements IPaths {
    
    private boolean[] marked;
    private int[] edgeTo;
    private final int s;
    
    public BreadthFristPaths(Graph g, int s) {
        marked = new boolean[g.V()];
        edgeTo = new int[g.V()];
        this.s = s;
        bfs(g, s);
    }
    
    private void bfs(Graph g, int s) {
        Queue<Integer> queue = new ListQueue<>();
        marked[s] = true;
        queue.enqueue(s);
        while (!queue.isEmpty()) {
            int v = queue.dequeue();
            for (int w : g.adj(v)) {
                if (!marked[w]) {
                    edgeTo[w] = v;
                    marked[w] = true;
                    queue.enqueue(w);
                }
            }
        }
    }
  
    @Override
    public boolean hasPathTo(int v) {
        return marked[v];
    }

    @Override
    public Iterable<Integer> pathTo(int v) {
        if (!hasPathTo(v)) return null;
        Stack<Integer> path = new ListStack<>();
        for (int x = v; x != s; x = edgeTo[x]) {
            path.push(x);
        }
        path.push(s);
        return path;
    }
}

深度优先搜索与广度优先搜索，都是图通用的搜索算法，搜索中，我们都会将起点存入数据结构，然后重复如下步骤：

1. 取其中的下一个顶点并标记。
2. 将v的所有相邻而又未被标记的顶点加入数据结构。

两个算法的不同之处在于从数据结构中获取下一个顶点的规则，广度优先是取最早加入的，深度优先则是取最晚加入的（递归隐式的包含一个stack，可以将dfs修改为使用stack的循环）。

private void dfsWithStack(Graph g, int v) {
        Stack<Integer> stack = new ListStack<>();
        stack.push(v);
        marked[v] = true;
        while (!stack.isEmpty()) {
            int node = stack.pop();
            for (int w : g.adj(node)) {
                if (!marked[w]) {
                    edgeTo[w] = node;
                    marked[w] = true;
                    stack.push(w);
                }
            }
        }
    }

连通分量

类似于unionfind，实现的思路也非常简单，我们以一个点作为起点，开始在图上进行深度搜索，将所有遍历过的点打上mark标记，同时将id数组均设置为count，然后对剩下的未标记的点逐一扫描，至多v()次就可以求出图中所有的连通分量。
api:

package algorithm.api;

public interface ICC {
    boolean connected(int v, int w);
    
    int count();
    
    int id(int v);
}

实现：

package algorithm;

import algorithm.api.ICC;
import define.Graph;

public class CC implements ICC {

    private boolean[] marked;
    private int[] id;
    private int count;

    public CC(Graph g) {
        marked = new boolean[g.V()];
        id = new int[g.V()];
        for (int s = 0; s < g.V(); s++) {
            if (!marked[s]) {
                dfs(g, s);
                count++;
            }
        }
    }

    private void dfs(Graph g, int s) {
        marked[s] = true;
        id[s] = count;
        for (int w : g.adj(s)) {
            if (!marked[w]) {
                dfs(g, w);
            }
        }
    }

    @Override
    public boolean connected(int v, int w) {
        return id[v] == id[w];
    }

    @Override
    public int count() {
        return count;
    }

    @Override
    public int id(int v) {
        return id[v];
    }
}

到现在为止，一件有意思的事情来了，unionFind 与 上面的cc都是将一堆的点进行分类，相互连通的放在一起，从功能逻辑上讲，二者是一致的，但二者基于不同的数据结构，实现功能有这不同的算法。
利用深度优先搜索算法，还可以干许多事情：
1.环问题：检测是否存在环 2.双色问题：能否用两种颜色区分图
环问题：

package algorithm;

import define.Graph;

/**
 * 环问题，其实就变得非常简单了，即等价于：在深度优先的遍历中是否遍历到起点。
 */
public class Cycle {
    private boolean[] marked;
    
    private boolean hasCycle;
    
    public Cycle(Graph g) {
        marked = new boolean[g.V()];
        for (int i = 0; i < g.V(); i++) {
            if (!marked[i]) {
                dfs(g, i, i);   
            }
        }
    }
    
    private void dfs(Graph g, int i, int u) {
        marked[i] = true;
        for (int w : g.adj(i)) {
            if (!marked[w]) {
                dfs(g, w, i);
            } else if (w == u) {
                hasCycle = true;
                break;
            }
        }
    }
    
    public boolean hasCycle() {
        return hasCycle;
    }
}

二色问题：

package algorithm;

import define.Graph;

/**
 * 二色问题，书上说等价于二分图，也就是下面的这个算法稍作修改可以找二分图。
 * 基本逻辑：
 * 遍历时 将子节点 标记为 ！父节点
 * 如果遇到已经遍历过的结点，就判断下颜色是否一致，一致则表示不能实现二分
 */
public class TwoColor {
    private boolean[] marked;
    private boolean[] color;
    private boolean isTwoColorable = true;

    public TwoColor(Graph g) {
        marked = new boolean[g.V()];
        color = new boolean[g.V()];
        for (int i = 0; i < g.V(); i++) {
            if (!marked[i]) {
                dfs(g, i);
            }
        }
    }

    private void dfs(Graph g, int i) {
        marked[i] = true;
        for (int w : g.adj(i)) {
            if (!marked[w]) {
                color[w] = !color[i];
                dfs(g, w);
            } else if (color[w] == color[i]) {
                isTwoColorable = false;
                break;
            }
        }
    }
    
    public boolean isBipartite() {
        return isTwoColorable;
    }
}

符号图

到目前为止，关于图的相关数据结构与算法均是用数字来表示结点，可实际中遇到的问题，更多的需要用字符串来表示。如何将字符串与我们前面所学的这些联系起来呢？自然需要建立一种映射关系，其背后所蕴含的思想与富豪表&hash等完全一致。在这种需求下，符号图应运而生。
api:

package algorithm.api;

import define.Graph;

public interface ISymbolGraph {

    boolean contains(String key);
  
    int index(String key);

    String name(int v);

    Graph g();
  
}

实现：

package algorithm;

import algorithm.api.ISymbolGraph;
import define.Graph;
import define.SequentialSearchST;
import define.SimpleST;
import edu.princeton.cs.algs4.In;

/**
 * 符号图的实现中
 * 一个符号表，用来保存，字符串与数字的映射
 * 一个字符串数组，充当反向索引，用来保存数字与字符串的映射
 * 一个数字表示结点的图
 */
public class SymbolGraph implements ISymbolGraph {
    private SimpleST<String, Integer> st;
    private String[] keys;
    private Graph g;

    public SymbolGraph(String stream, String sp) {
        st = new SequentialSearchST<>();
        In in = new In(stream);
        while (in.hasNextLine()) {
            String[] a = in.readLine().split(sp);

            for (int i = 0; i < a.length; i++) {
                if (!st.contains(a[i])) {
                    st.put(a[i], st.size());
                }
            }
        }
        
        
        keys = new String[st.size()];
        for (String name : st.keys()) {
            keys[st.get(name)] = name;
        }
        
        g = new Graph(st.size());
        in = new In(stream);
        while (in.hasNextLine()) {
            String[] a = in.readLine().split(sp);
            int v = st.get(a[0]);
            for (int i = 1; i < a.length; i++) {
                g.addEdge(v,st.get(a[i]));
            }
        }
    }

    @Override
    public boolean contains(String key) {
        return st.contains(key);
    }

    @Override
    public int index(String key) {
        return st.get(key);
    }

    @Override
    public String name(int v) {
        return keys[v];
    }

    @Override
    public Graph g() {
        return g;
    }
}

间隔的度数

间隔的度数问题，类似于六度理论，这里就不给代码实例了（我是如此的懒惰，书中没有的，自己绝不愿花时间来思考，并用那一句 完成比完美更重要 来作为自身行动力不足的佐证）。

1. 构造图
2. 图中寻找最短路径。

有向图

20240107-16:23：应该恭喜自己，终于走到了这里，我应该休息二十来分钟，然后将渺茫希望寄托于接下来的三小时左右。喂，喂，这一次可是别人将希望寄托于你呢，打起精神来！
有向图中，边变成单向的了，任何一条边所链接的两个顶点都是一个有序对，边的有向性，使得更贴合现实中的某些场景。这一看起来极为容易也颇为自然的改变，将会对算法产生深刻的影响（书中说的，到目前为止，我也没意识到将会有什么具体的影响）。为了说明边的方向性，而产生的细小文字差异所代表的结构特性正是本节的重点。
重点需要我们理解有向图中的可达性与无向图中的连通性，这两个概念的区别，概念上有向图明显更复杂一点，但我们表示有向图的数据结构甚至比无向图更简单。
api:

package define;

public interface IDigraph {
    
    int V();
    int E();
    void addEdge(int w, int v);
    Iterable<Integer> adj(int v);
    IDigraph reverse();
    
    String toString();
}

实现：

package define;

import define.impl.LinkBag;

public class Digraph extends AbstructDirectedGraph{
    
    private final int v;
    
    private int e;
    
    private Bag<Integer>[] adj;
    
    public Digraph(int v) {
        this.v = v;
        this.e = 0;
        this.adj = (Bag<Integer>[]) new Bag[v];
        for (int i = 0; i < v; i++) {
            adj[i] = new LinkBag<>();
        }
    }
    
    

    @Override
    public int V() {
        return v;
    }

    @Override
    public int E() {
        return e;
    }

    @Override
    public void addEdge(int w, int v) {
        adj[w].add(v);
        e ++;
    }

    @Override
    public Iterable<Integer> adj(int v) {
        return adj[v];
    }

    @Override
    public IDigraph reverse() {
        Digraph r = new Digraph(v);
        for (int i = 0; i < v; i++) {
            for (int w : adj[i]) {
                r.addEdge(w, i);
            }
        }
        return r;
    }
}

这份数据结构与无向图相比，唯一的区别只有addEdge,同时多个reverse方法。

可达性

在数据结构基本没什么差异的情况下，可达性这个其实跟无向图中的深度优先搜索算法也是没什么差异的。
api：

package algorithm.api;

public interface IDirectedDFS {
    boolean marked(int v);
}

实现：

package algorithm;

import algorithm.api.IDirectedDFS;
import define.Digraph;

public class DirectDFS implements IDirectedDFS {

    private boolean[] marked;

    public DirectDFS(Digraph g, int s) {
        marked = new boolean[g.V()];
        dfs(g, s);
    }

    public DirectDFS(Digraph g, Iterable<Integer> source) {
        marked = new boolean[g.V()];
        for (Integer i : source) {
            dfs(g, i);
        }
    }

    private void dfs(Digraph g, int s) {
        marked[s] = true;
        for (int w : g.adj(s)) {
            if (!marked[w]) {
                dfs(g, w);
            }
        }
    }

    @Override
    public boolean marked(int v) {
        return marked[v];
    }
}

相比于无向图中的深度优先算法，此处多了一个多点可达性的方法。
多点可达性的一个典型应用便是，内存系统，一个顶点表示一个对象，一条边表示对象对另一对象的引用。当某个对象入度为0时，则表示没有任何对象在引用他了，此时可以垃圾回收了（错误的，有可能为环，虽然入度不为0）。程序运行时，有些对象是可以访问的，而那些不用通过这些对象进行访问的对象就应该被回收掉。
广度优先算法的无向图实现也仅止需要将参数IGraph 修改为 IDigraph即可。
对于是否存在路径？最短路径等问题与有向图一致。

环与有向无环图

有向图的一个典型原型应用：优先级限制下的调度问题（课程与先导课程）。
而对于这类问题的一种解便是：拓扑排序。给定一幅有向图，将所有顶点排序，使得所有的有向边均从排在前面的元素指向排在后面的元素。
如果一个优先级限制的问题，存在环，则必然无解。

找环

有向图中找环与无向图类似，深度优先搜索算法如果遍历到了某个之前已经遍历到且就在本次调用栈上的结点，恭喜，环找到了。
api:

package algorithm.api;

public interface IDirectedCycle {
    boolean hasCycle();
    Iterable<Integer> cycle();
}

实现：

package algorithm;

import algorithm.api.IDirectedCycle;
import define.Digraph;
import define.Stack;
import define.impl.ListStack;

public class DirectedCycle implements IDirectedCycle {

    private boolean[] marked;
    private int[] edgeTo;
    private Stack<Integer> cycle;
    private boolean [] onStack;

    public DirectedCycle(Digraph g) {
        marked = new boolean[g.V()];
        edgeTo = new int[g.V()];
        onStack = new boolean[g.V()];
        for (int i = 0; i < g.V(); i++) {
            if (!marked[i]) {
                dfs(g, i);
            }
        }
    }

    private void dfs(Digraph g, int i) {
        marked[i] = true;
        onStack[i] = true;
        for (int j : g.adj(i)) {
            if (this.hasCycle()) {
                return;
            }else if (!marked[j]) {
                edgeTo[j] = i;
                dfs(g, j);
            }else if (onStack[j]) {
                cycle = new ListStack<>();
                for (int x = i; x != j; x = edgeTo[x]) {
                    cycle.push(x);
                }
                cycle.push(j);
            }
        }
        //递归返回的时候将其排除递归调用数组
        onStack[i] = false;
    }

    @Override
    public boolean hasCycle() {
        return cycle != null;
    }

    @Override
    public Iterable<Integer> cycle() {
        return cycle;
    }
}

优先级限制条件下的调度问题，等价于计算有向无环图中的所有顶点的拓扑顺序

顶点的深度优先次序

基本思想，深度优先的遍历中每个顶点都会被遍历且只会被遍历一次，所以我们在遍历的过程中将扫描到的顶点保存到一个队列中。于是顺序便有了。
典型的应用中一般如下三种排序：

1. 前序，递归调用之前将元素放入队列。
2. 后续，递归调用之后将顶点放入队列。
3. 逆后续，递归调用之后将顶点压入栈。

package algorithm;

import define.Digraph;
import define.Queue;
import define.Stack;
import define.impl.ListQueue;
import define.impl.ListStack;
import edu.princeton.cs.algs4.In;

public class DepthFristOrder {
    private boolean[] marked;
    private Queue<Integer> pre;
    private Queue<Integer> post;
    private Stack<Integer> reversePost;

    public DepthFristOrder(Digraph g) {
        pre = new ListQueue<>();
        post = new ListQueue<>();
        reversePost = new ListStack<>();
        marked = new boolean[g.V()];
        
        for (int i = 0; i < g.V(); i++) {
            if (!marked[i]) {
                dfs(g, i);
            }
        }
    }
    
    private void dfs(Digraph g, int i) {
        pre.enqueue(i);
        marked[i] = true;
        for (int j : g.adj(i)) {
            if (!marked[j]) {
                dfs(g, j);
                post.enqueue(i);
                reversePost.push(i);
            }
        }
    }
    
    public Iterable<Integer> pre() {
        return pre;
    }

    public Iterable<Integer> post() {
        return post;
    }

    public Iterable<Integer> reversePost() {
        return reversePost;
    }

}

拓扑排序

实际取得是深度优先算法中的逆后序。

package algorithm;

import define.Digraph;

public class Topological {
    private Iterable<Integer> order;

    public Topological(Digraph g) {
        DirectedCycle cycleFinder = new DirectedCycle(g);
        if (!cycleFinder.hasCycle()) {
            DepthFristOrder dfo = new DepthFristOrder(g);
            order = dfo.reversePost();
        }
    }

    public Iterable<Integer> order() {
        return  order;
    }

    public boolean isDGA() {
        return order != null;
    }
    
}

为什么逆后续就是拓扑排序呢？
深度优先的算法中，a结点返回了，然后才是b结点返回，那么按照方向顺序一定是先b再a，深度优先，先返回的一定是深度更深的。

有向图中的强连通性

首先定义强连通性：有向图中任意两个点都是相互可达的，则该图是强连通的。
两个顶点是强连通的，当且仅当，这两个顶点都在一个普通的有向环中。
有向图的强连通性是一种顶点之间的等价关系：
1.自反性
2.对称性：ab是强连通的，ba也是强连通的。
3.传递性：ab，bc，ac
强连通性将顶点分为了一些等价类，每一个等价类都是由相互均为强连通的顶点的最大子集组成，每一个子集都是有向图的强连通分量。（强连通分量是基于顶点来定义的）
如何求解强连通分量呢？通过给出一些已知条件外加部分的逻辑，引导并思考出下面的算法，以当前我的能力而言是远远不够的，所以这种时候强制性的记忆也不失为一种好办法😂。
api：

package algorithm.api;

public interface SCC {
    boolean stronglyConnected(int v, int w);

    int count();

    int id(int v);
}

实现：

package algorithm;

import algorithm.api.SCC;
import define.Digraph;

public class KosarajuSCC implements SCC {

    private boolean[] marked;
    private int[] id;
    private int count;

    public KosarajuSCC(Digraph g) {
        marked = new boolean[g.V()];
        id = new int[g.V()];
        DepthFristOrder order = new DepthFristOrder(g.reverse());
        for (int s : order.reversePost()) {
            if (!marked[s]) {
                dfs(g, s);
                count++;
            }
        }
    }

    private void dfs(Digraph g, int s) {
        marked[s] = true;
        id[s] = count;
        for (int w : g.adj(s)) {
            if (!marked[w]) {
                dfs(g, w);
            }
        }
    }

    @Override
    public boolean stronglyConnected(int v, int w) {
        return id[v] == id[w];
    }

    @Override
    public int count() {
        return count;
    }

    @Override
    public int id(int v) {
        return id[v];
    }
}

与无向图中寻找连通分量相比我们所做的小小改动仅仅是

for (int i = 0 ; i < g.v(), i++)

变成

for (int s : order.reversePost())

对上面算法的描述如下：
1.先计算反图的拓扑排序。
2.在图中进行标准的深度优先搜索，但要按照反图的拓扑顺序来遍历未被标记的顶点。
3.被同一个递归访问到的顶点都在同一个强连通分量中。
书中关于该算法的正确性解释没看懂，我这里给一个直观的理解（不能叫证明）
图g：1>2>3>4
反图：4>3>2>1
反图的逆后续：4>3>2>1
现在我们按照4321的顺序，深度优先访问图（1234），如果在对4进行深度优先访问时，标记了32则必然存在路径4-3-2，已经存在1234，现在又有了432，故 432是一个强连通。没有丝毫严谨可言，不过又有那么一点符合直觉。（2025-07-21 依旧没懂，不过，也不需要懂得每一个…）

有向图中的可达性

有向图g的传递闭包：相同顶点组成的另一幅有向图，必包中存在v-w的边，当且仅当g中v可以到达w。
api:

package algorithm.api;

public interface ITransitiveClosure {
    boolean reachable(int v, int w);
}

实现：

package algorithm;

import algorithm.api.ITransitiveClosure;
import define.Digraph;

public class TransitiveClosure implements ITransitiveClosure {

    private DirectDFS[] all;

    public TransitiveClosure(Digraph g) {
        all = new DirectDFS[g.V()];
        for (int i = 0; i < g.V(); i++) {
            all[i] = new DirectDFS(g, i);
        }
    }

    @Override
    public boolean reachable(int v, int w) {
        return all[v].marked(w);
    }
}

这不是一个可用于生产的算法，其需要构建从每个点出发进行深度优先算法的对象。所需要的空间与v平方成正比。

最小生成树

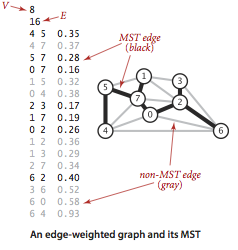
加权图：每条边关联了一个权重值/成本的图模型。
生成树：含有所有顶点的无环连通子图。
加权图的最小生成树：权值最小的生成树。
在计算最小生成树时，我们一般有如下默认的前提假设。

1. 只考虑连通图，不连通的图则叫最小生成森林。
2. 边的权重，可正，可负，可0，但不能相同。因为不同边权重相同，则最小生成树就不唯一了。

树的两个性质：

1. 用一条边连接树中任意两个顶点都会产生一个环。
2. 从树中删去任意一条边都会得到两个独立的树。

图的一种切分：将所有顶点分成两个非空且不重叠的集合，横切边就是连接两个属于不同集合顶点的边。
切分定理：一幅加权图中，给定任意的切分，其横切边中权重最小的必定属于最小生成树。
下面是cs61b中做的一点记录：
Minimum spanning tree is spanning tree of minimum total weight only in undirected graph as subgraph:

1. is connected
2. is acyclic
3. includes all of the vertices

1&2 determine it is tree,3 makes is spanning
是否存在某个顶点，其最短路径树，恰好是该图的最小生成树？–no
最短路径树，依赖于起始节点，而最小生成树是图的属性。

计算最小生成树：
Cut Property
最小交叉边，一定是最小生成树的一部分。（边如果不是唯一的，最小生成树也可能不是唯一的）
Prims Algorithm 有效具体实现：

类似dj，dj关注的是到源最短的路径，prim关心树的总权重，确定保留那一条路径的偏好不同，其余基本一致。 优先级队列，移除节点时，relax到非已确定点的边，决定保留那一条边。
Kruskal`s Algorithm:
边排序，从小到大，依次添加边直到v-1（避免环）；
优先级队列
不相交集：检测环
每次添加非环的边，可以理解为两个割中取最短。
切分定理是解决最小生成树问题的所有算法基础，这些算法都可以理解为一种贪心算法的特殊情况：
使用切分定理找到最小生成树的一条边，不断的重复直到找到最小生成树的所有边。

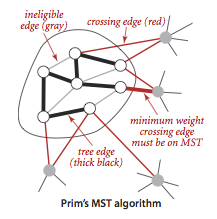
前面表示无向图&有向图 使用的数据结构核心都是邻接表数组，表示加权图时，稍有不同，我们新增了边这一对象，核心则是领接边数组。
无向加权图的数据结构-边：

package define;

public class Edge implements Comparable<Edge>{

    private final int v;
    private final int w;
    private final double weight;

    public Edge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public double weight() {
        return weight;
    }

    public int either() {
        return v;
    }

    public int other(int vertex) {
        if (vertex == v) return w;
        else if (vertex == w) return v;
        else throw new RuntimeException("不存在的点");
    }

    @Override
    public int compareTo(Edge o) {
        if (this.weight() < o.weight()) return -1;
        else if (this.weight() > o.weight()) return 1;
        else return 0;
    }

    public String toString() {
        return String.format("%d-%d %.2f", v, w, weight);
    }
}

无向加权图的数据结构-图：

package define;

import define.impl.LinkBag;
import edu.princeton.cs.algs4.In;

public class EdgeWeightedGraph {

    private final int v;
    private int e;
    private Bag<Edge>[] adj;

    public EdgeWeightedGraph(int v) {
        this.v = v;
        this.e = 0;
        adj = (LinkBag<Edge>[])new LinkBag[v];
        for (int i = 0; i < v; i++) {
            adj[i] = new LinkBag<>();
        }
    }

    public EdgeWeightedGraph(In in) {
        this(in.readInt());
        int e  = in.readInt();
        for (int i = 0; i < e; i++) {
            int v = in.readInt();
            int w = in.readInt();
            double weight = in.readDouble();
            Edge edge = new Edge(v, w, weight);
            adj[v].add(edge);
            adj[w].add(edge);
        }
    }

    public int v() {
        return v;
    }
    public int e() {
        return e;
    }
    public void addEdge(Edge e) {
        int v = e.either(),w = e.other(v);
        adj[v].add(e);
        adj[w].add(e);
        this.e++;
    }

    public Iterable<Edge> adj(int v) {
        return adj[v];
    }

}

我们已经定义了加权图的数据结构，now，start algorithm！

Prim算法

核心思想便是找权重最小的横切边。每次将下一条连接树中的顶点，与所有不在树中的顶点且权重最小的边加入树中
重点：使用一个优先队列来保存横切边，我们从优先队列中选择最小权重横切边时需要将已存在树中的边&两个顶点都在树中的边移除优先队列。

即时实现便是每一步都处理并移除失效的边。

延时实现则是边留在优先队列中，需要删除的时候再检查边的有效性。

更多的细节 -> show me code

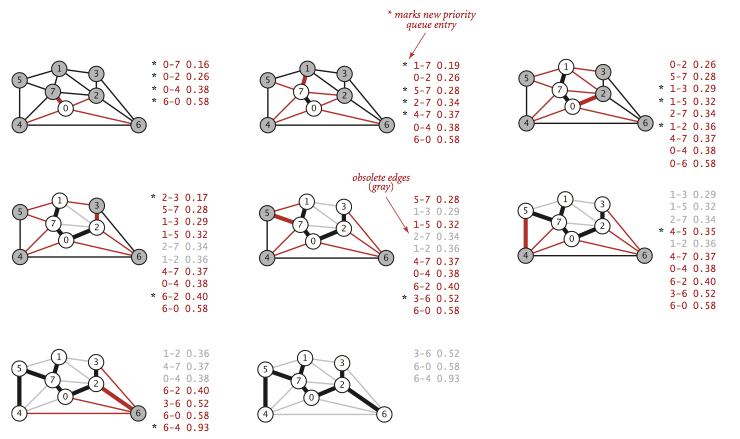
prim算法的延时实现：

package algorithm;

import define.Edge;
import define.EdgeWeightedGraph;
import define.Queue;
import define.impl.ListQueue;
import edu.princeton.cs.algs4.MinPQ;

public class LazyPrimMST {
    private boolean[] marked;//标记存在与树中的顶点
    private Queue<Edge> mst;//最小生成树的边。
    private MinPQ<Edge> pq;//横切边

    /**
     * 将当前顶点加入最小生成树，并将加入后与之相邻的边加入优先队列
     * @param g
     * @param v
     */
    private void visit(EdgeWeightedGraph g, int v) {
        marked[v] = true;
        for (Edge e : g.adj(v)) {
            if (!marked[e.other(v)]) pq.insert(e);
        }
    }
    
    
    public LazyPrimMST(EdgeWeightedGraph g) {
        pq = new MinPQ<>();
        marked = new boolean[g.v()];
        mst = new ListQueue<>();
        visit(g, 0);
        while (!pq.isEmpty()) {
            Edge e = pq.delMin();
            int v = e.either(), w = e.other(v);
            if (marked[v] && marked[w]) continue;//跳过失效的边，但不会将其从pq中移除
            mst.enqueue(e);
            if (!marked[v]) visit(g, v);
            if (!marked[w]) visit(g, w);
        }
    }
    
    public Iterable<Edge> edges() {
        return mst;
    }
    
    public double weight() {
        double rs = 0.0d;
        for (Edge e : mst) {
            rs += e.weight();
        }
        return rs;
    }
}

上面这个算法的主要耗时在于优先队列的插入与delMin。
对于上面的优化，从优先队列的角度出发，可以进行两次优化，1.我们只关心，非树顶点与树连接的边。2.在某一个非树顶点与树连接的边中，我们只关心权重最小的那条边，更多的实现细节：show me code
prim算法的即时实现：

package algorithm;

import define.Edge;
import define.EdgeWeightedGraph;
import define.IndexMinPriorityQueue;

public class PrimMST {
    private Edge[] edgeTo;//保存该点到树的权重最小的边，最终就是最小生成树的所有边。
    private double[] distTo;//edgeTo中对应边的权重。
    private boolean[] marked;//标记在树中的顶点。
    private IndexMinPriorityQueue<Double> pq; //保存横切边,数组下边对应的点对应的权重。
    
    
    private void visit(EdgeWeightedGraph g, int v) {
        marked[v] = true;
        for (Edge e : g.adj(v)) {
            int w = e.other(v);
            if (marked[w]) continue;
            if (e.weight() < distTo[w]) {
                edgeTo[w] = e;
                distTo[w] = e.weight();
                if (pq.contains(w)) {
                    pq.change(w, distTo[w]);
                } else {
                    pq.insert(w, distTo[w]);
                }
            }
        }
    }
    
    public PrimMST(EdgeWeightedGraph g) {
        edgeTo = new Edge[g.v()];
        distTo = new double[g.v()];
        marked = new boolean[g.v()];
        for (int i = 0; i < g.v(); i++) {
            distTo[i] = Double.POSITIVE_INFINITY;
        }
        pq = new IndexMinPriorityQueue<>(g.v());
        
        distTo[0] = 0.0;
        pq.insert(0, distTo[0]);
        while (!pq.isEmpty()) {
            visit(g, pq.delMin());
        }
    }
}

算法中，遍历当前最小权重新增加入树的顶点的所有关联边，对于关联边每一个涉及的顶点：
1.如果该顶点已在树中，则跳过。
2.如果该顶点，新的边权重小于已存在的边，更新edgeTo & distTo，同时如果优先队列中没有该顶点则加入优先队列（横切边），如果有，则更新该横切边的权重。
最终优先队列中只会保存横切边，且一个顶点只有一条（权重最小的那个）。
尽管延时&即时，数据结构不同，算法也有差异，本质都是找最小横切边然后加入最小生成树。

Kruskal算法

第二种算法的核心思想便是：将所有的边按权重排序，将最小的取出来，如果在已有的树中加入该边不构成环则将该边加入生成树。

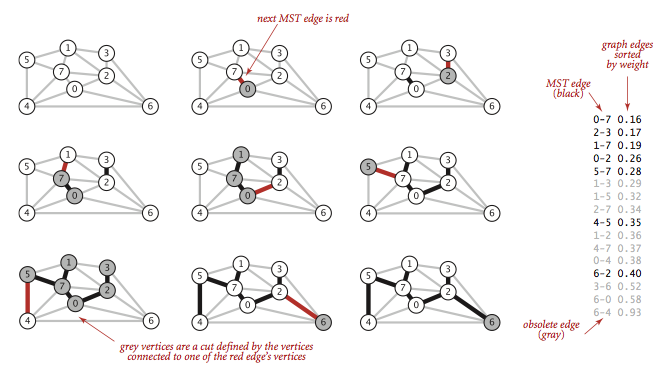
package algorithm;

import define.*;
import define.impl.ListQueue;
import edu.princeton.cs.algs4.MinPQ;

public class KruskalMST {
    private Queue<Edge> mst;

    public KruskalMST(EdgeWeightedGraph g) {
        mst = new ListQueue<>();//最小生成树中的边
        MinPQ<Edge> pq = new MinPQ<>();// 存放边的优先级队列
        for (Edge e : g.edges()) {
            pq.insert(e);
        }
        UnionFind uf = new WeightedQuickUnion(g.v());//用于判断点是已经存在与树中
        while (!pq.isEmpty() && mst.size() < g.v() - 1) {
            Edge e = pq.delMin();
            int v = e.either(),w = e.other(v);
            if (uf.connected(v, w)) continue;
            uf.union(v, w);
            mst.enqueue(e);
        }
    }
    
    public Iterable<Edge> edges() {
        return mst;
    }

}

最短路径

终于开始向这周计划中的最后的堡垒开始进攻了，关于最小生成树部分，精力一点都不集中，囫囵吞枣般勉强算是完成了，对于我的第一篇真正意义上的长篇，一定要完成全部的内容！那就速战速决！
作为地理背景出身的人，对最短路径相关问题的最先想到的就是，arcgis中的路径分析，地图中的找路。最短路径模型最直观的便是路径问题，地图&网络等，也有任务调度，以及似乎与图，没有任何关系的套汇问题。
我们研究的重点是单点最短路径问题，假设涉及的都是有向加权强连通图，那么结果就是一棵固定了根节点的最短路径树。
最短路径问题的背景是有向加权图，so，先介绍有向加权图的数据结构。基本可以参考加权图的数据结构实现，唯一不同的则在于边是有向的。

有向加权图

有向加权边：

package define;

public class DirectedEdge {
    private final int v;
    private final int w;
    private final double weight;

    public DirectedEdge(int v, int w, double weight) {
        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public double weight() {
        return weight;
    }

    public int form() {
        return v;
    }

    public int to() {
        return w;
    }

    public String toString() {
        return String.format("%d->%d %.2f", v, w, weight);
    }
}

有向加权图：

package define;

import define.impl.LinkBag;

public class EdgeWeightedDigraph {
    private final int v;
    private int e;
    private Bag<DirectedEdge>[] adj;

    public EdgeWeightedDigraph(int v) {
        this.v = v;
        this.e = 0;
        adj = (Bag<DirectedEdge>[]) new Bag[v];
        for (int i = 0; i < v; i++) {
            adj[i] = new LinkBag<>();
        }
    }

    public int v() {
        return v;
    }
    public int e() {
        return e;
    }
    public void addEdge(DirectedEdge e) {
        adj[e.form()].add(e);
        this.e++;
    }

    public Iterable<DirectedEdge> adj(int v) {
        return adj[v];
    }

    public Iterable<DirectedEdge> edges() {
        Bag<DirectedEdge> bag = new LinkBag<>();
        for (int i = 0; i < this.v; i++) {
            for (DirectedEdge e : adj[i]) {
                bag.add(e);
            }
        }
        return bag;
    }
}

最短路径api

package algorithm.api;

import define.DirectedEdge;

public interface SP {
    double distTo(int v);
    boolean hasPathTo(int v);
    Iterable<DirectedEdge> pathTo(int v);
}

在介绍具体的算法前，可以回顾下前面的广度优先搜索。
实现最短路径算法的核心概念：松弛（relaxation）
边的松弛：放松边 v -> w 意味着检查s到w的最短路径，是否是先从s到v，然后由v到w，是则更新相关数据结构。

private void relax(DirectedEdge e) {
  int v = e.from(),w = e.to();
  if (distTo[w] > distTo[v] + e.weight()) {
    distTo[w] = distTo[v] + e.weight();
    edgeTo[w] = ve;
  }
}

顶点的松弛：放松从顶点指出的所有边，逐条检查。

private void relax(EdgeWeightedDigraph g, int v) {
  for (DirectedEdge e : g.adj(v)) {
    int w = e.to();
    if (distTo[w] > distTo[v] + e.weight()) {
      distTo[w] = distTo[v] + e.weight();
      edgeTo[w] = e;
    }
  }
}

松弛操作，可以找到最短路径的理论证明：
命题：当且仅当，对于v到w的任意边e，都满足distTo[w] <= distTo[v] +e.weight()时，他们是最短路径。
必要性（满足b一定要有a）：最短边，一定满足公式，反证法，存在大于，则一定可以用当前替换大于。
充分性（a 推 b）：满足公式的就是最短边。
1.公式推导出：distTo[w] <= e1.weight() + … + ek.weight() = OPT(sw);
2.任何一条边的路径一定是大于等与最短边的
综合：OPT(sw) <= distTo[w] <= OPT(sw) 等价 distTo[w] = OPT(sw);
通用算法：放松所有边，直到不存在有效边为止。

Dijkstra算法

最早接触dj算法是计算机网络中的路由部分，严格讲我已经接触了至少三次，对其的模糊印象只有：
1.选一个点开始，获取其所有边。
2.选边中权重最小的，将其纳入edgeTo数组。
可以理解为 有向加权图中的制定起点的最小生成树路径。二者一大差异便是，prim中每次添加的是距离树最近的顶点，dj算法则是添加的距离起点最近的顶点。一个distTo[w]中统计的是 w到树的权重，一个统计的是w到起点的权重。
看到dj算法，才意识到prim算法的重要性！而在上午学习prim算法时，根本没用脑…

package algorithm;

import define.DirectedEdge;
import define.EdgeWeightedDigraph;
import define.IndexMinPriorityQueue;
import define.Stack;
import define.impl.ListStack;

public class DijkstraSP {
    
    private DirectedEdge[] edgeTo;
    private double[] distTo;
    private IndexMinPriorityQueue<Double> pq;
    
    public DijkstraSP(EdgeWeightedDigraph g, int s) {
        edgeTo = new DirectedEdge[g.v()];
        distTo = new double[g.v()];
        pq = new IndexMinPriorityQueue<>(g.v());
        
        for (int i = 0; i < g.v(); i++) {
            distTo[i] = Double.POSITIVE_INFINITY;
        }
        distTo[s] = 0.0D;
        pq.insert(0, distTo[s]);
        while (!pq.isEmpty()) {
            
        }
    }
    
    private void relax(EdgeWeightedDigraph g, int v) {
        for (DirectedEdge e : g.adj(v)) {
            int w = e.to();
            if (distTo[w] > distTo[v] + e.weight()) {
                distTo[w] = distTo[v] + e.weight();
                edgeTo[w] = e;
                if (pq.contains(w)) {
                    pq.change(w, distTo[v] + e.weight());
                } else {
                    pq.insert(w, distTo[w]);
                }
            }
        }
    }
    
    public double distTo(int v) {
        return distTo[v];
    }
    
    public boolean hasPathTo(int v) {
        return distTo[v] < Double.POSITIVE_INFINITY;
    }
    
    public Iterable<DirectedEdge> pathTo(int v) {
        Stack<DirectedEdge> stack = new ListStack<>();
        for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.form()]) {
            stack.push(e);
        }
        return stack;
    }
}

注意：dijkstra算法，解决的是非负权重的加权有向图中最短路径问题。

加权无环有向图-求最短路径

将拓扑排序与求最短路径结合起来，便是加权无环图中找。

package algorithm;

import define.DirectedEdge;
import define.EdgeWeightedDigraph;

public class AcyclicSP {
    private DirectedEdge[] edgeTo;
    private double[] distTo;

    private void relax(EdgeWeightedDigraph g, int v) {
        for (DirectedEdge e : g.adj(v)) {
            int w = e.to();
            if (distTo[w] > distTo[v] + e.weight()) {
                distTo[w] = distTo[v] + e.weight();
                edgeTo[w] = e;
            }
        }
    }

    public AcyclicSP(EdgeWeightedDigraph g, int v) {
        edgeTo = new DirectedEdge[g.v()];
        distTo = new double[g.v()];
        for (int i = 0; i < g.v(); i++) {
            distTo[i] = Double.POSITIVE_INFINITY;
        }
        distTo[v] = 0.0;

        Topological top = new Topological(g);
        for (int v : top.order()) {
            relax(g, v);
        }

    }
}

这个算法是不能直接运行的，因为没有对拓扑排序兼容。
为什么按照拓扑排序，运行顶点放松就能找到最短路径呢？
获取最短路径的核心思想便是 distTo[w] <= ditsTo[v] + e.weight();那么要想从w作为起点开始找下一个结点时，必须要固定s到w的值，而所有指向w的边都可能改变distTo[w]的值。
dj的做法是选当前所有横切边中与s最短的那个（w），纳入最短路径树。因为非负，如果还有其他路径到w比当前更短，则其他路径必然会经过当前所有横切边中非选中的某条，当某条已经比当前选中的更长了。
拓扑排序则会让我们在将w作为起点前，遍历所有指向w的边，及此时distTo[w] 一定是固定了的，我们已经从他的所有可能性中选出了最短的那个。
拓扑排序后的顶点放松算法，已经没有任何提高的空间了（书中所言）。

加权无环有向图-求最长路径

只需要图中权重取反后求最短即可。

加权无环有向图-并行任务调度

前面的拓扑排序，解决了单一处理器情况下的优先级限制任务调度问题，现实中往往是团队作业，那么我们所面临的便是，优先级限制下的并行任务调度。咋一看与我们的有向无环图没有任何联系（到目前为止，我也没想到将二者结合起来的逻辑抽象）。
书中提及，“关键路径”的方法，可以证明该问题与无环加权有向图的求最长路径等价：
优先级限制下的任务调度，可以简单转化为无环有向图，如果将每一任务的完成所需时间作为权重，便是无环有向加权图，在这幅图中，长度则是：完成路径所有任务的最早可能时间。
具体的由优先级任务构建有向无环图的的步骤与算法详见《算法》p430。
拓展（没理解）：相对最后期限限制下的并行任务调度
a任务必须要在b任务开始的n个时间单位内开始，等价于，b任务必须要早于a任务n个时间内开始。

一般加权有向图中的最短路径问题

这里的限制条件则是，有负数权重，并且可能存在环。dj不能处理负数，拓扑排序&松弛点无法解决环。
当图中存在负权重时，我们可能为了经过负权重而绕弯，这种效应需要我们将查找最短路径的感觉转变为对算法本质的理解，需要抛弃直觉并在一个更加抽象的层面上考虑这个问题。
负权重环
在有向加权图中，所有s到w的路径上经过的点都不存在于任何负权重环时，s到w的最短路径才是存在的。
下面先给一些约束，以减轻算法的复杂度。
1.起点不可达的顶点，最短路径为正无穷。
2.起点可达，但路径上某个顶点属于负权重环，则最短路径为负无穷。
3.对于其他所有顶点，计算最短路径树&权重。
现在需要我们解决的问题转化为：
1.负权重环的检测
2.负权重环不可达时的单点最短路径
bellman-ford算法的理论证明，没看懂…
对于没看懂的东西，处理起来总是很不甘心的，就像是在做一种无用功，似乎曾经干过某事，如此这般。
不能描述其证明，为什么么这样做是对的，只能描述一下算法本身，也觉得没有余力继续深入下去了。
当我们，改变了某一个点的distTo值，从这个点指出的其他相关点的distTo 都会收到影响，需要重新判断。故我们是用一个队列来辅助，对w点的distTo做修改时，将受其影响的所有点加入队列（如果该点队列中已经存在则忽略）只要队列不为空，且不存在负权重环，就一直不停的从队列中取点relax。
没看懂，挖个坑，后面埋。

20240116:不想埋，直接开始字符串部分吧。

###