• Whatever the assignment, start now.
• Yes, that’s really all there is.
• Don’t fight the problem.
• Practice is important. Don’t just assume you can do it; do it!
  
  programming means a great deal more, including
  
  
  1. Design of what programs do.
  2. Analysis of the performance of programs.
  3. Confirmation of their correct operation.
  4. Management of their complexity.

编程就是对复杂性的管理

other

A key principle in software development is that it is generally better for code to crash than produce an incorrect result

python debug：

1. doctest: python3 -m doctest lab1.py
2. print & boolean print
3. assert

装饰器模式
为什么不这样呢？

def aFunc1(x):
...
aFunc = trace1(aFunc1)

这样就不适用于函数的内部调用，如果afunc1 是递归调用，则内部调用没有trace1.
python中的多变量：

x,y = 10,11

L=[(a,b),(c,d)]
for x,y in L:
  pass

S = [a,b,c]
for x,y in zip(range(1,4),S):
  pass

破坏性操作 & 非破坏性操作 Destructive & non-destructive
是否改变了原始属性。
nonlocal & global:
方法内的非全局&全局的非全局，
You cannot update a variable in the global frame using nonlocal
抽象界限
可变与不可变
== & is：identity & equality
is None & type(a) is type(b)
python在处理 小数子&字符串时 也会搞一些内存优化

current = 0
def count():
  curent = current + 1  # error
  print("current:",current) #only this is ok
  
current = []
<br>
def append(name):
  current.append(name) # ok
  
"""
python 看见赋值= 就会创建一个局部变量 current 而其没有初始化 就参与 current+1 的计算了

to slove:
global & nonlocal
Avoiding global:
"Just because you can do something in a language, it doesn't mean you should." - Prof Fox

Re-assigning global variables inside functions can lead to more brittle and unpredictable code.
"""

We say that an object is mutable if its state can change as code is executed. The process of changing an object’s state is called mutation.
复习：抽象界限？
通用求值逻辑：

1. Evaluate the operator to get a procedure.
2. Evaluate each of the operands from left to right.
3. Apply the value of the operator to the evaluated operands.

Name&Value

三个基本的组成：

• Values are data we want to manipulate and in particular
• Functions are values that perform computations on values
• Expressions denote computations that produce values.
  值，函数也是值，函数的内容=表达式，表达式可以理解为函数这个值的具体内容 在状态机模型中：
  
  1. 一个初始状态
  2. 一些控制状态流转的指令
     从这个角度来理解编程语言：值（定义初始状态）+ 表达式（定义状态流转）这两个就是基础，在python中我们进一步抽象了函数的概念，函数是特殊的值，封装了表达式，可以用来对其他值进行计算。
     
     
     函数定义：

def axbc(a,b,c):
  return a*b+c

匿名函数： 匿名函数怎么用呢？

lambda a,b,c:a+b+c

对于函数这个value的基本操作就是：call / invoke

print(axbc(1,2,3))

Puer function（纯函数）: their output depends only on their input parameters’ values, and they do nothing in response to a call but compute a value. Impure function（非纯函数）: may do additional things when called besides returning a value, have side effect.

print(*vals)

Most side-effects involve changing the value of some variable.

from random import randint
randint(0,100)
randint(0,100)

两次调用randint方法，参数一致的情况下，返回结果不一致，一定是改变了内部某个变量（时间？seed？）。 print方法，可以理解为每次调用，改变了 打印出来的那个变量的值。
use the hidden-variable idea to describe side effects when doing formal mathematical descriptions of programming languages.
软件工程中一般认为，不可见的副作用是不安全的，尽量避免。
To evaluate a function call:

1. Evaluate the operator, and then the operands (from left to right).
2. Apply the operator to the operands (the values of the operands).
   表达式，作为函数这个value的具体内容，可以抽象为：Operator(operand1,operand2)，即操作符&操作数。
   对表达式的解析是一个递归的调用过程：

add(add(1,2),add(3,4))

如前面所述：一些字面意义上的value比较容易理解，一些函数/变量意义上的value，则难以理解
Deduction（演绎）: there must be another source of information.演绎一定是从前提信息（another source of information）中推理获取新的信息。
Python如何定义value呢？(python如何定义初始状态呢)

1. assignments of values to names;a=1
2. function definitions;def abc(x,y):return x+y;def本身就是一个赋值，将function a(x,y)… 赋值给a ,a就代表着这个函数
3. parameter passing to functions

def fun(x):
  def f(x):
    return x
  return f

fun(5)(6)
'''
返回 6
为什么return 里面的x 的 value 是6 而不是 5 呢？
为什么会把外面的x给屏蔽掉呢？
'''

对于上述疑问的解释需要引入新的概念：Environments（name space）

Environments

环境就是 name – value的映射；在这个环境中，value 绑定到这个 name上 。

对value的解释，要在环境的定义下才有意义

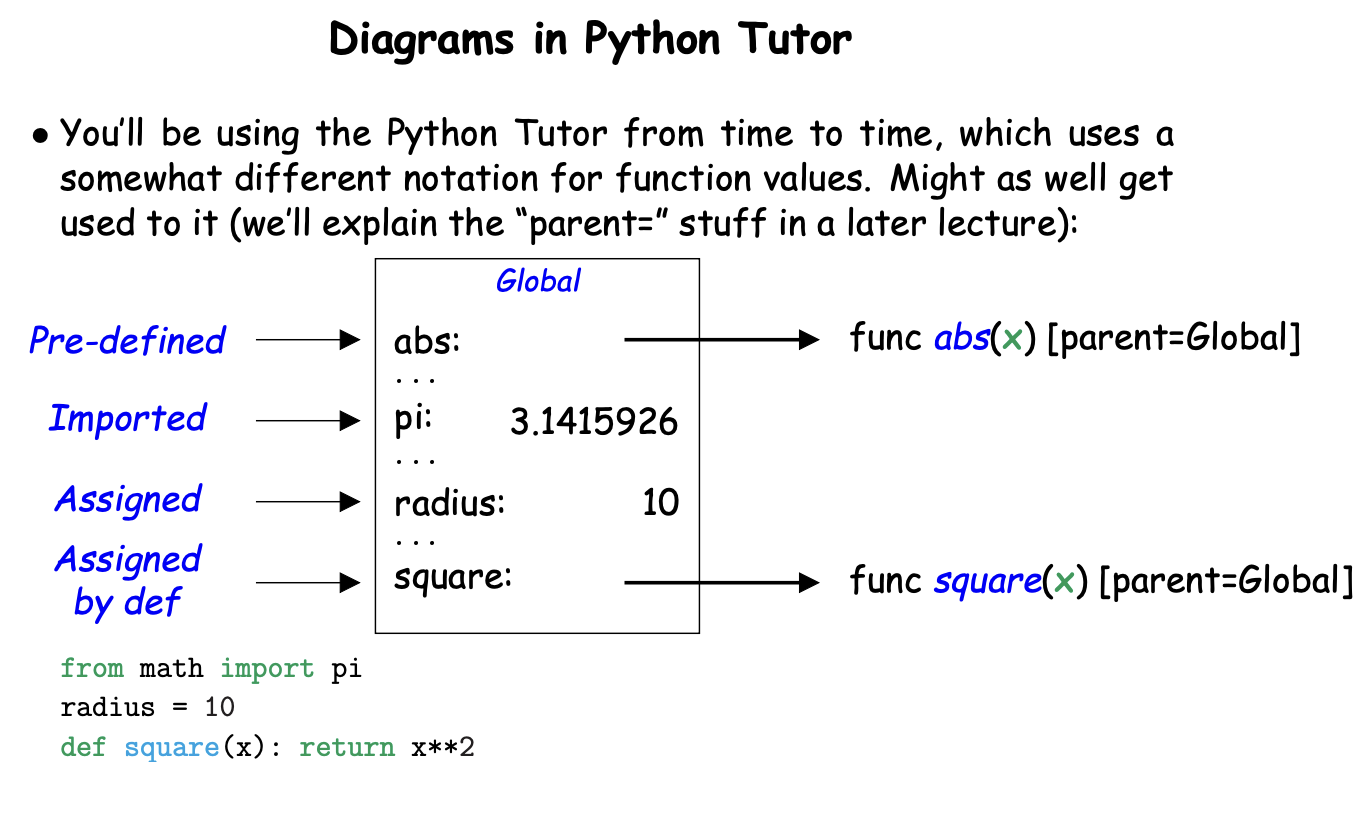
Evaluation: 求值

1. 当我们对变量赋值时，会在当前求值框架下，创建一个新的绑定。
2. 每次获取都是在环境中获取最新的值。
3. 隐藏：当我们寻找name的meaning时，会从环境链中逐次寻找，stop at frist one。

Remember that programs are simply a set of statements, or instructions

Control

如果让机器人帮你做作业，那学习的就是机器人了，而不是你。

a = 1
b = 2

def abc(x,y):
  return x + y

"""
environment:global
maping:
name:a value:1 
name:b value:2
name:abc value: function abc(x,y)[parent = global]

通常：这个由 函数+代码+父环境 组成的东西 我们叫 “闭包”
"""

前面介绍的expressions（操作符&操作数）是按顺序求值的（evaluate），control expression则是控制 操作数的求值顺序的。

语句（statement），与表达式不同，他们只 do 不求值，no value，通常被单独用来副作用。control statement 则是用来控制 do 的执行顺序。
executed statement & evaluated expressions
1.if

"""
In Python, to evaluate
TruePart if Condition else FalsePart
– First evaluate Condition.
– If the result is a “true value,” evaluate TruePart; its value is then
the value of the whole expression.
– Otherwise, evaluate FalsePart; its value is then the value of the
whole expression.
"""

1/x if x != 0 else 0

2.

if condition:
	do
elif condition:
	do
else:
	do

3.Iteration

while & recursive

4.short-circuit evaluation

false and (condition)

后面的condition 不会计算，like java

"""
python 三元表达式
"""
def wears_jacket(temp, raining):
    return True if temp < 60 or raining else False
  
"""
if...  if...\if...elif...else...\if...return if... return 
"""

Higher Order Function

函数： domain 定义域 range 值域 codomain 上域/陪域 陪域是最大的那个值域，值域是陪域的一个子集
Two Design Principles：

• Functions should do one well-defined thing（一个方法只干一件事）
• DRY (Don’t Repeat Yourself).

高阶函数可以理解为函数的模板，参数name 的 value 是函数，用于构造函数的函数。

def summation(N, term):
	k = 1
	sum = 0
	while k <= N:
		sum += term(k)
		k += 1
	return sum

def square(x):
	return x*x
summation(5, square)

#also summation(5, lambda x: x*x)

#next : a more complex example

def combine_funcs(op):
   def combined(f, g):
       def val(x):
           return op(f(x), g(x))
       return val
   return combined
from operator import add
add_func = combine_funcs(add)
from math import sin, cos, pi
h = add_func(sin, cos)
h(pi / 4)

thunks ：指针碰到栈底的声音😂

这里的不可能，是因为传递expression给函数时，就已经会预先求值了，除非通过thunks这种形式的函数，将表达式包装进函数里面，从而实现，只调用其中一个而不是所有。作为函数的operand 其必须最终是一个值（neither value or function，not statement ）

"""
>>> fn1 = lambda:1/x
>>> print(fn1)
<function <lambda> at 0x1033c6ef0>
>>> def iffunc(a,b,c):
... return a() if b else c()
  File "<stdin>", line 2
    return a() if b else c()
    ^
IndentationError: expected an indented block after function definition on line 1
>>> def iffunc(a,b,c):
...     return a() if b else c()
... 
>>> print(iffunc)
<function iffunc at 0x1033c7010>
>>> fn2 = iffunc(fn1,True,lambda:0)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 2, in iffunc
  File "<stdin>", line 1, in <lambda>
NameError: name 'x' is not defined
>>> x = 2
>>> fn2 = iffunc(fn1,True,lambda:0)
>>> print(fn2)
0.5
>>> 

注意无参lambda定义的fn1；iffunc在运行时需要在其环境指定变量x。即fn1中的x不是通过函数参数传入而是读取的环境中的变量。
"""

几个经典例子：

def f():
  return 0

def g():
  print(f())
  
def h():
  def f():
    return 1
  g()
  
# h() 的打印结果是 ：0
# 因为h函数调用了全局变量中的g函数，g函数只能读取全局变量中的f函数，不能读取定义在h中的f函数。注意与java的多态区分。

def f(p, k):
	def g():
		print(k)
	if k == 0:
		f(g, 1)
	else:
		p()
f(None, 0)

#注意递归中，第一次调用f(None,0) 与第二次f(g,1) 其父框架均是global，this is rule
#f(g,1) 中调用的p()是参数传递进来的，而不是在本次调用中定义的！
# result：0

最经典的错误例子！：

def f(x):
	def g(y):
		x = y
	g(4)
	return x
print(f(3))

#still 3, g中的x（=4）与父环境中的x（=3）没有任何关系。
#因为x=y的赋值操作，x是在g函数中新建的变量而不是外部环境中的x

def f(x):
	def g(y):
		print(x)
	g(4)
	return x
print(f(3))
#输出两次3

非常经典的一个例子：利用环境

def div_by_primes_under(n):
    """
    计算i是否能被小于n的数整除
    >>> div_by_primes_under(10)(11)
    False
    >>> div_by_primes_under(10)(121)
    False
    >>> div_by_primes_under(10)(12)
    True
    >>> div_by_primes_under(5)(1)
    False
    """
    checker = lambda x: False
    i = 2
    while i <= n:
        if not checker(i):
            checker = (lambda f, i: lambda x: x % i == 0 or f(x))(checker, i)
        i = i + 1
    return checker

def div_by_primes_under_no_lambda(n):
    """
    >>> div_by_primes_under_no_lambda(10)(11)
    False
    >>> div_by_primes_under_no_lambda(10)(121)
    False
    >>> div_by_primes_under_no_lambda(10)(12)
    True
    >>> div_by_primes_under_no_lambda(5)(1)
    False
    需要重点理解
    """
    def checker(x):
        return False
    i = 2
    while i <= n:
        if not checker(i):
            def outer(f, i):
                def inner(x):
                    return x % i == 0 or f(x)
                return inner
            checker = outer(checker, i)
        i = i + 1
    return checker
  
#翻译div_by_primes_under_no_lambda（5）（7）
#7 % 5 ==0 or 7 % 3 == 0 or 7 % 2 == 0 or False
"""
init : checker : False
i = 2 运行完checker : x % 2 == 0 or False
i = 3 运行完checker : x % 3 == 0 or x % 2 == 0 or False
i = 4 false 不更新checker
i = 5 运行完checker : x % 5 == 0 or x % 3 == 0 or x % 2 == 0 or False
...
if not checker(i)语句：如果一个数不能整除以比它小的任何素数，那么这个数就是素数
"""

这里的几道练习实在太经典了：

def get_k_run_starter(n, k):
    """
    >>> get_k_run_starter(123444345, 0) # example from description
    3
    >>> get_k_run_starter(123444345, 1)
    4
    >>> get_k_run_starter(123444345, 2)
    4
    >>> get_k_run_starter(123444345, 3)
    1
    >>> get_k_run_starter(123412341234, 1)
    1
    >>> get_k_run_starter(1234234534564567, 0)
    4
    >>> get_k_run_starter(1234234534564567, 1)
    3
    >>> get_k_run_starter(1234234534564567, 2)
    2
    """
    i = 0
    final = None
    while i <= k:
        while n % 10 > (n // 10) %10:
            n = n // 10
        final = n % 10
        i = i + 1
        n = n // 10
    return final

def best_k_segmenter(k, score):
    """
    >>> largest_digit_getter = best_k_segmenter(1, lambda x: x)
    >>> largest_digit_getter(12345)
    5
    >>> largest_digit_getter(245351)
    5
    >>> largest_pair_getter = best_k_segmenter(2, lambda x: x)
    >>> largest_pair_getter(12345)
    45
    >>> largest_pair_getter(245351)
    53
    >>> best_k_segmenter(1, lambda x: -x)(12345)
    1
    >>> best_k_segmenter(3, lambda x: (x // 10) % 10)(192837465)
    192
    """
    partitioner = lambda x: (x // 10**k, x % 10 ** k)
    def best_getter(n):
        assert n > 0
        best_seg = None
        while n:
            n, seg = partitioner(n)
            if best_seg == None or score(seg) > score(best_seg):
                best_seg = seg
        return best_seg
    return best_getter

def div_by_primes_under(n):
    """
    >>> div_by_primes_under(10)(11)
    False
    >>> div_by_primes_under(10)(121)
    False
    >>> div_by_primes_under(10)(12)
    True
    >>> div_by_primes_under(5)(1)
    False
    """
    checker = lambda x: False
    i = 2
    while i <= n:
        if not checker(i):
            #checker = (lambda f, i: lambda x: x % i == 0 or f(x))(checker, i)
            # 为什么下面这种写法是错误的？
            checker = (lambda x: x % i == 0 or checker(x))
        i = i + 1
    return checker

def div_by_primes_under_no_lambda1(n):
    """
    >>> div_by_primes_under_no_lambda(10)(11)
    False
    >>> div_by_primes_under_no_lambda(10)(121)
    False
    >>> div_by_primes_under_no_lambda(10)(12)
    True
    >>> div_by_primes_under_no_lambda(5)(1)
    False
    """
    def checker(x):
        return False
    i = 2
    while i <= n:
        if not checker(i):
            
            def inner(x):
                return x % i == 0 or checker(x)
                
            checker = inner
        i = i + 1
    return checker

def div_by_primes_under_no_lambda(n):
    """
    >>> div_by_primes_under_no_lambda(10)(11)
    False
    >>> div_by_primes_under_no_lambda(10)(121)
    False
    >>> div_by_primes_under_no_lambda(10)(12)
    True
    >>> div_by_primes_under_no_lambda(5)(1)
    False
    """
    def checker(x):
        return False
    i = 2
    while i <= n:
        if not checker(i):
            def outer(f, i):
                def inner(x):
                    return x % i == 0 or f(x)
                return inner
            checker = outer(checker, i)
        i = i + 1
    return checker

def three_memory(n):
    """
    >>> f = three_memory('first')
    >>> f = f('first')
    Not found
    >>> f = f('second')
    Not found
    >>> f = f('third')
    Not found
    >>> f = f('second') # 'second' was not input three calls ago
    Not found
    >>> f = f('second') # 'second' was input three calls ago
    Found
    >>> f = f('third') # 'third' was input three calls ago
    Found
    >>> f = f('third') # 'third' was not input three calls ago
    Not found
    """
    def f(x, y, z):
        def g(i):
            if x == i:
                print("found")
            else:
                print("not found")
            return f(y, z, i)
        
        return g
    
    return f(None, None, n)

Recursion

总是以为自己掌握了递归…

def printsums(n):
	print(n)
	def nextsum(k):
		return printsums(n+k)
	return nextsum
print sums(1)(3)(5)
"""
1, print(1) and return func:nextsum
2, nextsum(3) invoke printsums(1+3) then print(4) return nextsum
3, nextsum(5) invoke printsums(4+5) then print(9) retuen nextsum
一个值在当前环境中没有被定义，但是在父环境中被定义了，也是可以引用的
"""

方法的哲学：
每一个方法都有一个标签（signature） 标签也可以理解为 语法说明（名称&参数）,指明了如何调用该方法。
语义说明则由两部分构成
​ 1. 前置条件：对调用者的约束 ​ 2. 后置条件：方法实现者的保证（这个方法会返回给你什么)
进一步分解则是：

1. 调用者只考虑，提供参数&使用结果，不关心方法实现
2. 方法实现者，只考虑如何compute result，不关心参数的提供&结果的使用
3. 从客户端的角度，signature 就是一系列可能计算出结果的方法的抽象概念。用了ta就能得到想要的结果。
   Programming is largely about choosing abstractions that lead to clear, fast, and maintainable programs
   Programming = 选择抽象概念，实现 整洁 & 快速 & 可维护 的程序。
   线性递归 与 尾递归
   
   

#liner recursions
def sum_squares(n):
    if n < 1 :
        return 0
    else :
        return n**2 + sum_squares(n-1)
"""
else 返回n**2 及「n-1 到 1平方和」而这正好符合 sum_squares的语义。
"""

#loop
def sum_squares(n):
    accum = 0
    k = 1
    while k <= n:
        accum = accum + k**2
        k += 1
    
    return accum
     
#tail recursions
def sum_squares(n):
    def part_sum(accum, k):
        if k <= n:
            return part_sum(accum + k**2, k+1)
        else:
            return accum
    
    return part_sum(0, 1)

官方证实：递归与循环是可以互相转换的🤔，尤其是尾递归，几乎有固定的公式来进行转换。

线性递归，需要将每一步算出来的值保存到stack中，直到base case 才开始返回，并从stack取出。由大到小。 尾递归，每一次递归都将上一次算出的值带入本次，无需额外的stack保存。由小到大。
递归，信念跳跃：

Tree Recursion

尾递归/线性递归，意味着一次只会调用一个递归方法。

尾递归，意味着递归调用之后没有其他操作了。这里虽然只会调用一个is_a_zero但如果为false还会继续 func(middle)…

一个很好的例子：need more think

计数

运行时，每一步是怎么走的呢？– 深度优先搜索
如果说前面的例子让你稍微领略了一点点递归的魅力🤩，下面则给了我一种简直是魔法的感觉。
初步看到这个问题时，压根不知道如何求解，而答案竟是如此的简单…

def num_partitions(n, k):
  """
  返回，n可以通过多少种正整数求和来表达，其中每一个正整数都 <=k & k>0 & empty sum = 0
  """
  if n < 0:
    return 0
  elif k == 1:
    return 1
  else:
  	return num_partitions(n-k, k)+num_partitions(n, k-1)

Example:
num_partitions(6, 3):
6
= 3+3
=3+2+1
=3+1+1+1
=2+2+2
=2+2+1+1
=2+1+1+1+1
=1+1+1+1+1+1
总共7种，answer = 7；
分成两个递归，一个是k逐渐变小：
3+3
2+2+2
1+1+1+1+1+1
一个是k不变的情况下细化内部成员：
3+3
3+2+1
3+1+1+1
即使到现在，依然觉得解题答案十分巧妙，模拟了几次运行，依然不得要领…😭
Now more interesting recursion:
Tower of Hanoi:
一碟盘子，三根柱子，按照由大到小整齐码在一根柱子上，现在需要将其移动到另外一根柱子。
要求：每次只能移动一个 & 堆叠必须满足大的在下，小的在上。
solution：

1. 现实中模拟操作
2. 将操作书写成步骤

一个盘子：直接将其移动到目标盘子。
多个盘子：
​ 将k-1个盘子移动到空余柱子
。 ​ 将最大的那个移动到目标柱子。
​ 将k-1个盘子从空余柱子移动到目标柱子。
？ 为什么不是现实中的一个盘子一个盘子移动，而是整体k-1 个盘子呢
def hanoi_tower(n, target)，因为方法的语义便是将n个盘子移动到目标柱子
3.将步骤翻译成代码

def hanoi_tower(n, start, end):
  """
  语义
  """
  if n == 1:
    move(start, end)
  else :
    spare = 6 - start - end
    hanoi_tower(n-1, start, spare)
    move(start, end)
    hanoi_tower(n-1, spare, end)

# 简单，整洁，如此强大！

4.我在看过课程后，写出来了，但我依然无法在大脑中直接构建出每一步骤。so try to simulate operation
Removing Digits：
从一个数字中移除指定的数字

def remove_digit(n, k):
  """
  >>> remove_digit(123435, 3)
  1245
  """
  if n == 0:
    return 0
  if n % 10 == k:
    return remove_digit(n // 10, k)
  return n % 10 + remove_digit(n // 10, k) * 10
    

都是如此的简洁&强大，而我却写不出😭
Do not worry if you struggle with these problems, it is okay to struggle while learning.😂😂
关于递归的经典练习太多了，而又是如此的不幸，几乎每一道都做不出来…

def make_repeater(func, n):
    """Return the function that computes the nth application of func.

    >>> add_three = make_repeater(increment, 3)
    >>> add_three(5)
    8
    >>> make_repeater(triple, 5)(1) # 3 * 3 * 3 * 3 * 3 * 1
    243
    >>> make_repeater(square, 2)(5) # square(square(5))
    625
    >>> make_repeater(square, 4)(5) # square(square(square(square(5))))
    152587890625
    >>> make_repeater(square, 0)(5) # Yes, it makes sense to apply the function zero times!
    5
    """
    "*** YOUR CODE HERE ***"
    def f(x):
        i = n
        while i :
            x = func(x)
            i -= 1

        return x
    
    return f

def cycle(f1, f2, f3):
    """Returns a function that is itself a higher-order function.

    >>> def add1(x):
    ...     return x + 1
    >>> def times2(x):
    ...     return x * 2
    >>> def add3(x):
    ...     return x + 3
    >>> my_cycle = cycle(add1, times2, add3)
    >>> identity = my_cycle(0)
    >>> identity(5)
    5
    >>> add_one_then_double = my_cycle(2)
    >>> add_one_then_double(1)
    4
    >>> do_all_functions = my_cycle(3)
    >>> do_all_functions(2)
    9
    >>> do_more_than_a_cycle = my_cycle(4)
    >>> do_more_than_a_cycle(2)
    10
    >>> do_two_cycles = my_cycle(6)
    >>> do_two_cycles(1)
    19
    """
    "*** YOUR CODE HERE ***"
    funl = [f1, f2, f3]
    def func1(n) :
        
        def func2(x):
            if n == 0: return x
            return funl[(n-1) % 3](func1(n-1)(x))
   
        return func2

    return func1

def cs61nay(combiner, n):
    """ Return a function that takes n arguments,
    one at a time, and combines them using combiner.
<
    >>> f = cs61nay(lambda x, y: x * y, 3)
    >>> f(2)(3)(4) # 2 * 3 * 4
    24
    >>> f(-1)(2)(3) # -1 * 2 * 3
    -6
    >>> f = cs61nay(lambda x, y: x - y, 4)
    >>> f(1)(2)(-2)(-1) # 1 - 2 - -2 - -1
    2
    >>> f = cs61nay(lambda x, y: x + y, 1)
    >>> f(61)
    61
    >>> f(2021)
    2021
    """
    def func(x):
        if n == 1:
            return x
        else:
            return lambda m : cs61nay(combiner,n-1)(combiner(x, m))
    
    return func

这三道练习题非常经典，除了第一个外，剩余两个都没有做出来…

1. 重复调用func n次
2. 总共调用n次，但却是 f1,f2,f3循环调用
3. 我们无法构建类似f(f(f(x))) 这样的形式，直观的combine(x, nay(combine, n-1)()…),但n ！=1 时其返回的是一个函数，不是value。n控制次数，但每一次实际的combine 这写在外面。
   
   
   

Abusing the Call Stack

i failed ，and no answer…
如何利用高阶函数，实现数据保存？

# 完全用匿名函数，实现递归：递归，重复调用表达式，可以将表达式作为函数参数

def make_anonymous_factorial():
    """Return the value of an expression that computes factorial.

    >>> make_anonymous_factorial()(5)
    120
    >>> from construct_check import check
    >>> # ban any assignments or recursion
    >>> check(HW_SOURCE_FILE, 'make_anonymous_factorial', ['Assign', 'AugAssign', 'FunctionDef', 'Recursion'])
    True
    """    
    def func1(x):
        if x == 1:
            return 1
        else:
            return x * func2(x-1)
        
    def func2(x):
        if x == 1:
            return 1
        else:
            return x * func1(x-1)
    
    #将函数理解为一段表达式，f1 & f2 是一样的，等效于 递归
        
    
    #将需要递归的函数表达式作为参数
    def func3(f, x):
        if x == 1:
            return 1
        else:
            return x * f(f, x-1)

    return func3(lambda f, x: 1 if x == 1 else x * f(f, x-1))

    return (lambda f:lambda x: f(f,x)) (lambda f, x: 1 if x == 1 else x * f(f, x-1))

Recursion Think

A recursive function is a function that calls itself in its body, either directly or indirectly. Recursive functions have three important components:

1. Base case(s), the simplest possible form of the problem you’re trying to solve.
2. Recursive case(s), where the function calls itself with a simpler argument as part of the computation.
3. Using the recursive calls to solve the full problem.

写出有效递归的一些tips：

1. recursive leap of faith.：相信自己，函数是有效的！
2. 从简单的版本开始。
3. 将最简单的情况作为base_case ，递归的大部分错误就是basecase找错了。
4. 也许可以先写出循环的版本。

书写递归的三个普遍步骤：

1. Figure out your base case
2. Make a recursive call with a simpler argument
3. Use your recursive call to solve the full problem

Tree Recursion

树递归，就是递归方法调用自己超过一次。

一个挑战：

判断一个数是不是质数，同时使用 前面碰到的规则进行优化（一个数如果不能被所有小于他的质数整除，则就是质数），前面是在哪里碰到的这个练习呢？scip 整理数种不同类型的递归！😭😭

"""
Q7: (Tutorial) Count K
Consider a special version of the count_stair_ways problem, where instead of taking 1 or 2 steps, we are able to take up to and including k steps at a time. Write a function count_k that figures out the number of paths for this scenario. Assume n and k are positive.
"""

def count_k(n, k):
    """ Counts the number of paths up a flight of n stairs 
    when taking up to and including k steps at a time. 
    >>> count_k(3, 3) # 3, 2 + 1, 1 + 2, 1 + 1 + 1
    4
    >>> count_k(4, 4)
    8
    >>> count_k(10, 3)
    274
    >>> count_k(300, 1) # Only one step at a time
    1
    """
    "*** YOUR CODE HERE ***"
    if n < 0 :
        return 0
    elif n == 0:
        return 1
    else :
        sum = 0
        for i in range(1, k+1):
            sum += count_k(n-i, k)

        return sum
      #2025-07-16 : 整理文档时解决！ yes！yes！ 

又一个习题：挑战失败…，完全没有思路。感觉要卡死在这里了…

Exception

Try …
Except …
Else…
Finally…
Raise …
Assert…
balabala…

Containers and Sequences

我们已知的这些简单的概念，究竟可以构造出多复杂的东西出来？ let·s try！
我们尝试用当前已知的东西，构建 pair 这个数据结构p<a, b>

上面这个，进入pair_func时，因为赋值语句，会直接创建本地变量 a = None & b = None，如果此时 which == 0，返回未赋值的 a 会直接报错。

fix：声明 a & b 是 nonlocal 的

上面的例子，展示了如何用一些基础特性，构建复杂特性，但实际中python 提供了一些容器，作为数据的数据。

now start intercept sequences：

list于tuple的主要区别：tuple 不可变，list可变！

字符串：sequence of string

1. 单/双 引号
2. 字符串中可以直接使用编码
   …
3. r字符串 表示原始字符串，无需转义等
   
   

sequence 的选择与切片

sequence 的组合与转换

sequence的迭代：循环

sequence 的一些其他语法

def match(a,b):
  return sum([1 for x,y in zip(a,b)]);
	return sum([a[x] == b[x] for x in range(len(a))]);
	# next both woring!!!
  # 因为下面的表达式 match("abc","acb") = 3
	return len([(x,y) for x in a for y in b if x == y]);
	return len([0 for x in a for y in b if x == y]);

Data Abstraction

ADT: abstract data type
API:

1. 60s 我们把程序理解为一系列的过程拆解
2. 70s 则强调哪些被方法操作的数据的流转
3. adt 代表了一些data 以及在这些data上的操作
4. 我们通常在一堆adt里面管理程序
5. 对于每一个type 我们定义api 来描述可以进行哪些操作
6. 通常api 则是由function 组成的
7. The collection of specifications (syntactic and semantic) of these functions constitutes a specification of the type.
8. 之所以是抽象的，因为client 不需要知道adt的细节。知道adt的specification就行
   
   

对于每个adt的api，一般分类三类（构造&get&set)：

1. constructors
2. accessors
3. mutators
   Dictionaries, Matrices, and Trees
   
   Dict:可变的mapping of key-value pairs
   
   

name = {
  "SCIP":"计算机程序的构造与解释",
  "CSAPP":"深入理解计算机系统"
}

key：必须是不可变的类型
value：可以是任何类型
Matrices:
矩阵：多种方式实现…
Trees:

Iterator

l = [a,b,c]
itor = iter(l)

netx(itor)

l.__iter__()

迭代器会跟踪元素，但只会跟踪到创建时的长度。

Generator

迭代器的一种
use yield instand return
运行到 找不到 yeild
暂停程序 while 而不是重新运行
递归生成树：

Object&Class

class Product:
  
  	#Set the initial values
    _tax = 1.11
    
    # 类似Java 构造器
    # 第一个参数是对象自己，也可以用其他替换，ex：this
    def __init__(self, name, price, nutrition_info):
      self._name = name
      self._price = price
      self._nutrition_info = nutrition_info
      self._inventory = 0
      
    # Define methods
    def incr_inventory(self, amount):
      self._inventory += amount
    
    
  product_a = Product("name",1.99, ["24 g sugar"])
  
  #两种调用方式
  product_a.incr_inventory(2)
  Product.incr_inventory(product_a, 2)

Inheritance + Composition

class Animal:
  def __init__(self, name, age = 0):
    self.name = name
    self.age = age
    
    def eat(self, food):
      print(f"xxxx eat {food}")
  
class Elephant(Animal):
  def eat(self, food):
    if food == "meat":
      super().eat(food)
      #Animal.eat(self, food)
    else:
      print(f"elephant eat {food}")
  

继承
重写
调用父类方法
调用父类构造器
python 也是所有类继承object

aclass.__class__.__bases__

Object

__str__  #返回对象的字符串形式 ， 人类可读

__repr__ #返回对象的字符串形式 ， 计算机可读

eval #求值  eval(rerp(...))

id()

getattr(buuy, "ear", False)
__getattribute__(self, name)

hasattr()

#python . 实际调用的都是 dunder方法

Recursive Object

Tree & Linked List

Complex

抛开各种具体的环境 & 执行细节，为了更一般的测量：strategic vagueness.
将注意力集中在 操作的次数上。
结果为一个比值，会大概告诉我们，随着n成比例的增加，计算机处理所需要的时间是如何成比例增加的。
从精确的时间 –> 函数是如何增长的

Sometimes, results for “small” values are not indicative
we tend to ask about asymptotic behavior of programs: as size of input goes to infinity

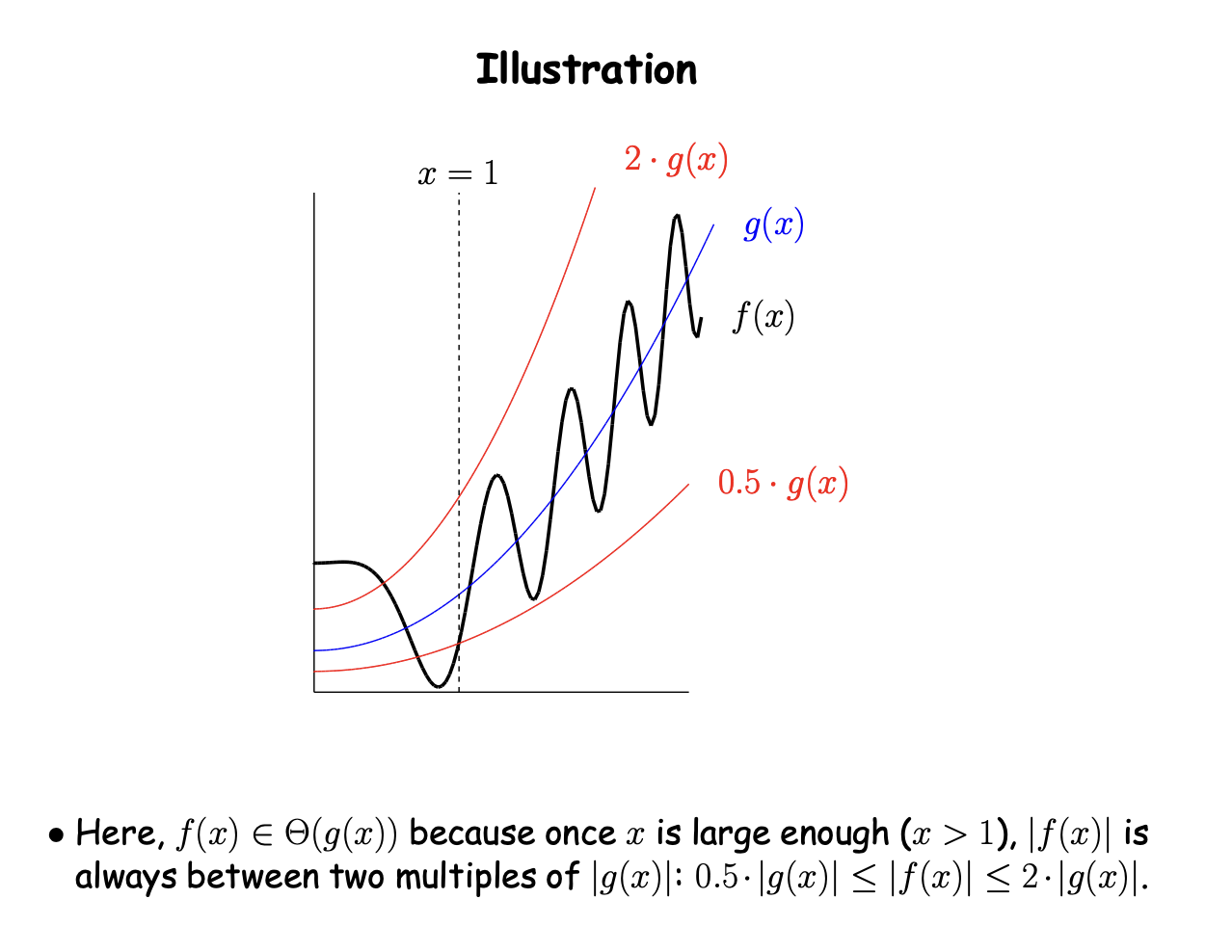
big O： f(x) <= kO(g(x))
big theta: k1(g(x)) < f(x) < k2 * (g(x))

Recursion & Memoization

非常困，至少假努力一下，乱七八糟的过完今天计划过的课程…
下面这个是非常经典的递归，即使前面写过一次，依旧没吃透理解
动态规划

Generics

格式化字符串输出，just 百度吧
%s
format
f string
泛型，python也有泛型？python有类，但没有类型呀 curious!
因为python没有类型，so 实际上python的函数参数都是泛型的。只要参数满足表达式用到的行为
__ iter __:
__ add __: 重载 +
python 可以自定义 操作符
join 函数
sorted & sort()


Record：
20240324，晴，差10分中午13点。
最近突然变得比较糟糕了，作业不想做，也没什么状态去做，cs61a也有点不想看了，似乎完全没法推进下去。今天甚至都想在家打一天手游，还好自己坚持来了，有必要对过去的那些暂时放一下，开始scheme。感觉很难放松，睡眠也总是不好，不能有效的休息，进一步导致精力不足，恶性循环了。也许我做不到100%，甚至80%都做不到。god 60万岁吧，调整状态，休息甚至是一门非常重要的学问。start 吧，三节课，以及配套的练习，今天的target！！！

Scheme

​ 我们将用schem来演示应用级程序的 范式计算（没有副作用，没有赋值，全是非破环性的操作），因此也不会使用赋值&可变数据结构，没有副作用，将会使得编程更加简单，同时副作用与可变性，让并发编程变得更加的困难！
let‘s start：

scheme 基本数据结构

学习任何一门语言都必须了解这门语言操作的值是什么
We divide Scheme data into atoms and pairs.

schem 应用程序本身就是其操作值。pair：pair of pair
quote ‘ 表示引用（这是一个字符串），而不是求值
一些例外：
if/and/or

cond

define/lambda

“ + - * / quotient”

cons car cdr

= / eq / eqv / equal

let

scheme中的递归

python 中每一次调用return 都需要进入下一个调用，直到base case 再层层返回最终求值（占用额外的stack空间），但再scheme中则会每次翻译下次调用的表达式，当翻译到最后一个时，求完值，答案也就出来了，不需要再层层返回。

always go easy stuff frist，so that you can get your brownie point，don‘t be embarrassed that you are saying some obvious，because is has to be said after all

Calculator

机器语言
程序语言：提供了一些抽象，把我们从机器语言中解放出来。

The Halting Problem and Incompleteness

通过标题，完全不知道接下来将要讲什么
halt problem:
存在一些输入，能让程序进入无限循环当中？
存在一个程序能分析代码并回答上述问题吗？
answered：no


什么是证明：
如果我们能通过给符号添加足够多的限制来获取我们想要的属性，那么我们就可以通过语法操作来表示大量杂乱的意义。（通过对有限定理的操作，我们可以完成对大量具体事务的抽象表达）

公理：前置约束
公理模式：一个代表无穷多公理的模板
证明：以我们所需证明的语句作为有限的一系列语句的结尾。这一系列语句，要么是公理，要么是模板的实例。
三段式

可以通过编写一个程序来判断，哪些是公理，哪些是模板的实例，即通过给定的公理等可以穷举出所有可以证明的命题（大英博物馆算法？）
通过编码，将字符转化成数字，
失败：没懂！！！！ failed，despair。

Macros-define syntax

一个早有听过，但从未去了解过的概念/主题：宏

百度中的概念：宏就是一些命令组织在一起，作为一个单独命令完成一个特定任务
宏更像是一种替换

执行程序之前的条件编译

是否可以理解为，宏就是提供了一种替换，因为先于程序执行，所以可以替换程序中函数的实现，同时因为是替换，不存在函数中的参数求值，等等

Declarative Programming

声明式编程，aha，一个全新的概念！

我们的程序主要是命令式的，程序由命令组成，这些命令告诉我们如何执行某些计算。

声明式编程：程序描述所需结果的特征，让系统去计算如何得到这些。fantastic，我要什么，然后让计算机去想办法获取结果。

One current version is programming by example, in which one gives examples of desired results and tries to get the system to generalize this into an algorithm.

输入：定义对象+其所允许的操作+想要的结果
输出：达到结果所需要的一系列操作
prolog
fact & rule

已知：fact
rule：如上
x是z的父亲，如果我们能证明z是y的祖先，我们就可以得到结论：x是y的祖先

prolog中我们不定义方法，定义 关系：

3与-3的关系是abs

封闭宇宙假设： 我们只做肯定的陈述。我们最接近于说某件事情是虚假的，就是说我们无法证明它。

amazing thing

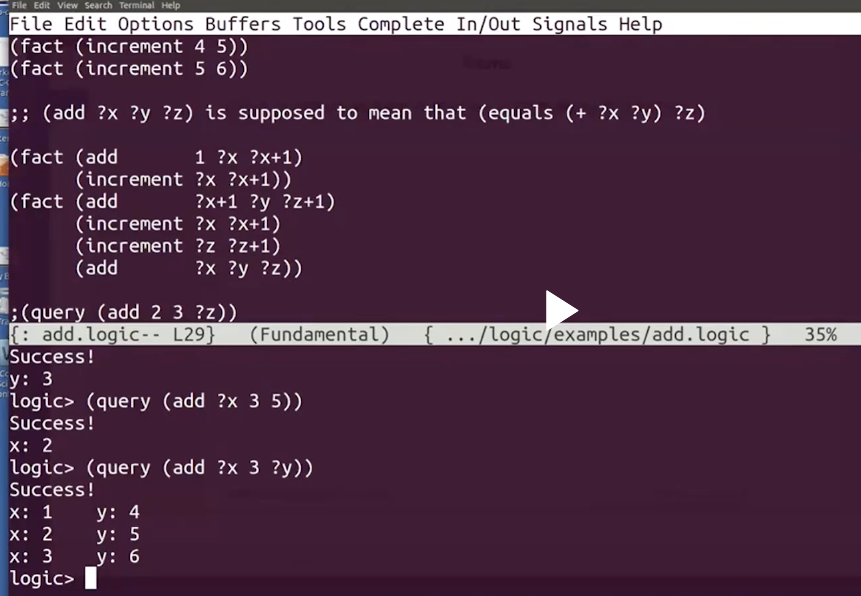
声明事实
定义加法
得到诸多结论

More information：课本的4.5节

Regular Expressions

来点也比较有意思的，正则表达式，模式匹配，非确定有限状态自动机。一种声明式编程

• We can think of this as a kind of declarative programming, because the programmer is saying, e.g., “find somethin that looks like this” rather than “search for the substring ‘(’, then look for a ’)’ after that” to check for a parenthesized expression.

我们给定的字符串是模式的子字符串吗？

python中模式的\ 与字符串的转义通常冲突，所以一般用原始字符串表示模式r”\s” ，不过\不能出现在字符串末尾，原始字符串不允许末尾有\。r”
”= \


关于正则表达式的具体内容，算法第四版的介绍已经足够了

一些python的语法：

mat = re.match mat = re.fullmatch mat = re.search boolean(mat) mat.group()/mat.groups()，括起来的模式，（括号）不仅可以分组，还可以通过group检索各部分

遇到矛盾的时候，python 解析第一个

mat = re.match(r'wind|window', 'window')
mat.group()
#'wind'

贪婪匹配

惰性匹配

BNF

巴科斯范式 one more concept
Algol 60 介绍了描述编程语言的标准语法方式，现在我们使用bnf范式去描述。
bnf是一个比正则表达式更加强大的模式语言。

邱奇理论，type 0/1/2
bnf简介

Lark
使用bnf定义sentences：

数字：可以是一串数字+“，”+ 一个数字 ｜ 一个数字

正则表达式无法描述这种括号，bnf范式 描述：

BNF的语法结构：

Conclusion

Project: Interpreter

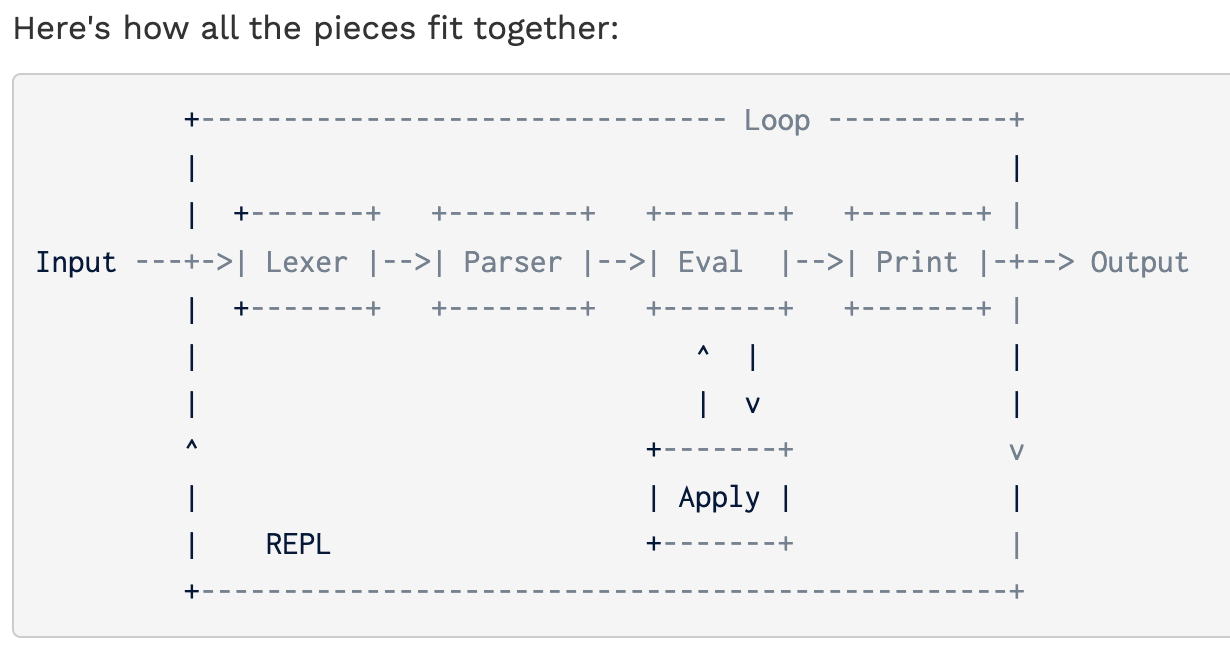
Many interpreters use a Read-Eval-Print Loop (REPL). This loop waits for user input, and then processes it in three steps:

1.Read :
解释器读取用户输入& passes it through a lexer and parser.
lexer：将输入的字符串转化为底层实现语言的“原子单位”（atomic pieces (tokens)）that are like “words” of the implemented language.
parser：将token组织进底层语言能够理解的数据结构
2.Eval:
eval 与 apply 之间相互递归，求值表达式&得到value
Eval takes an expression and evaluates it according to the rules of the language. Evaluating a call expression involves calling apply to apply an evaluated operator to its evaluated operands.
Apply takes an evaluated operator, i.e., a function, and applies it to the call expression’s arguments. Apply may call eval to do more work in the body of the function, so eval and apply are mutually recursive.
3.Print：
Display result

在正式开始项目前，lab11非常有意思，在定义好了类与职责后，完美的再现了求值过程中的递归，即使表达式几乎看不到一丁点的递归的代码影子！如此精巧与简洁，simple code huge power ！每次看这些总是觉得自己一直以来写的是什么鬼东西啊…