CS61b

Software Engineer:
Complexity Defined:
Complexity is anything related to the structure of a software system that makes hard to understand modify the system.

如何定义复杂性（Symptoms of Complexity）:


软件很少被物理条件限制，几乎是一个纯粹的创造性活动，最大的限制是对我们所构建的东西的理解。
1.代码简单并直观，消除特例。hiding complexity
2.封装到模块。modular design
The best modules are those whose interfaces are much simpler than their implementation.
The best modules are those that provide powerful functionality yet have simple interfaces,i use term deep to describe such modules.simple interfaces do complicated thing.
!!avoid over-reliance on ‘temporal decomposition’;时间上的先后顺序并不等同于逻辑上的先后顺序。
!!be strategic,not tactical;
重点关注信息泄露：什么是编程中的信息泄漏？

Java中的值：

1.基本类型声明：
变量及之后的一串比特空间
应用类型：
new ：开创一块比特空间，并返回地址（64bit address）（my treasure is no.1312312312th)；
基本类型的变量，后面跟着对应的比特空间；
引用类型的变量，后面跟着64bit地址空间，all 0=null；
裸递归
单向链表-sentinel
双向链表-two sentinel。 circle list
array – size*2. loiter
inheritance:
hypernyms 上位词
hyponym 下位词
Dynamic method:
Step1:compile time determine signature s of the method to be called;
​ s is decided using only static types
Step2:run time invoking object`s signature s;

Managing complexity:
Hierarchical abstraction:

• ​ create layers of abstraction with clear abstraction barriers!
  “Design for abstraction”(D.parnas)”
  
• ​ Organize program around objects
  
• ​ Let objects decide how things are done
  
• ​ Hide information others don`t need

继承对封装的破环：
Super：method1(){method2} method2(){…}
Subclass: overrider method2(){method1}
自己的method2 调用父类的method1 父类method1 又调用自己的method2
原本安全的封装变得不安全了
Higher Order Functions:高阶函数，以其他函数为数据的函数
java没有函数类型，不允许存在指针指向函数
传统方式：通过接口来实现

q1：子类与父类有相同名称的变量？
q2：子类与父类拥有相同 signature 的方法？静态方法没有overrid
two practices to solve – hiding （？）（不提倡)
comparable–>Natural Order
other order –> comparator
==:compare bits。for references means address
一些好的demo：

public static IntList of(int ...argList) {
        if (argList.length == 0)
            return null;
        int[] restList = new int[argList.length - 1];
        System.arraycopy(argList, 1, restList, 0, argList.length - 1);
        return new IntList(argList[0], IntList.of(restList));
    }

public static boolean squarePrimes(IntList lst) {
        // Base Case: we have reached the end of the list
        if (lst == null) {
            return false;
        }

        boolean currElemIsPrime = Primes.isPrime(lst.first);

        if (currElemIsPrime) {
            lst.first *= lst.first;
        }

        return currElemIsPrime || squarePrimes(lst.rest);  // java 一个为真就不会再去计算后面的表达式了
    }

Section2:
An engineer will do for a dime what any fool will do for a dollar;
Efficient :
1.Programming cost(help method!)
2.Excution cost
Measure Computational Cost:
Operation times –> cost model –> simplification–>order of growth
Formalize:Big-Theta

Big O: … less than or equal O(?);

Find strategies:
1.Find exact sum
2.Write out examples
3.Draw pictures
Common Big O:

1. Recursion :2的n次方
2. Binary Search:log以2为底n的对数～logN
3. Merge Sort:merge(比较两个数组中最小的一个，按顺序将两个数组进行合并)，将数组直接从1开始一直合并NlogN
4. 1,2,2,4,4,4,4,8,8,8,8,8,8,8,8,16. N(1:1;2:1+2;3:1+2;4:1+2+4;5:1+2+4)

(自适应排序)
ADT: Abstract Data Types. Defined only by its operations not by implementation;
Stack:filo. 堆内存：系统分配，比较小； link & array
GrabBag:(insert, remove,sample,size); array

1.Disjoint Sets

Inverse acrmen function;
不相交集合/并查集 的核心功能：（connect）（isConnected）
Implement：

1. 追踪每一个点及边
2. ListOfSetsDS
3. QuickFindDS:数组存储id
4. QuickUnionDS:数组存储parentid
   1. WeightedQuickUnionDS:新增权重（数量）（1.并行数组维护，2.将root标识为数量的负数）来确定谁合并到谁。（以数量作为权重与树的高度作为权重差异不大）
   2. WeightedQuickUnionWithPathCompressionDS:每一次isConnected 将修改链路上的元素的parentid

2.Binary Search Trees

(Skip List?)
Define:
Tree:

1. A set of nodes;
2. A set of edges that connect those nodes(only one path exists between two nodes);

Rooted Tree:

1. one node is root;
2. Every node have only one parent except root;
3. no child node is leaf;

Rooted Binary Trees:

1. every node has either 0,1 or 2 children;

Binary Search Trees:

1. Rooted Binary Trees;
2. Left means less,Right means greater;
3. can`t have duplicate key;

Operations:

1. search
2. insert
3. delete

3.B-Tree

Worst case BST hight is O(N);
Height,Depth,Performance:
Depth:distance of node to root;
Height: deepest leaf; worst runtime to find a node;
Average depth:(node-num*depth)/sum(node);
Good news:random operation BST ~ O(log(N))
Bad news:neraly cant operate random; data comes in over time;

B-tree:avoiding imbalance;
1.hight no change; – leaf become leaves;
2.leaf nodes avoid too juice;– limit ,over limit give one to parent(left middle)
So Wired:

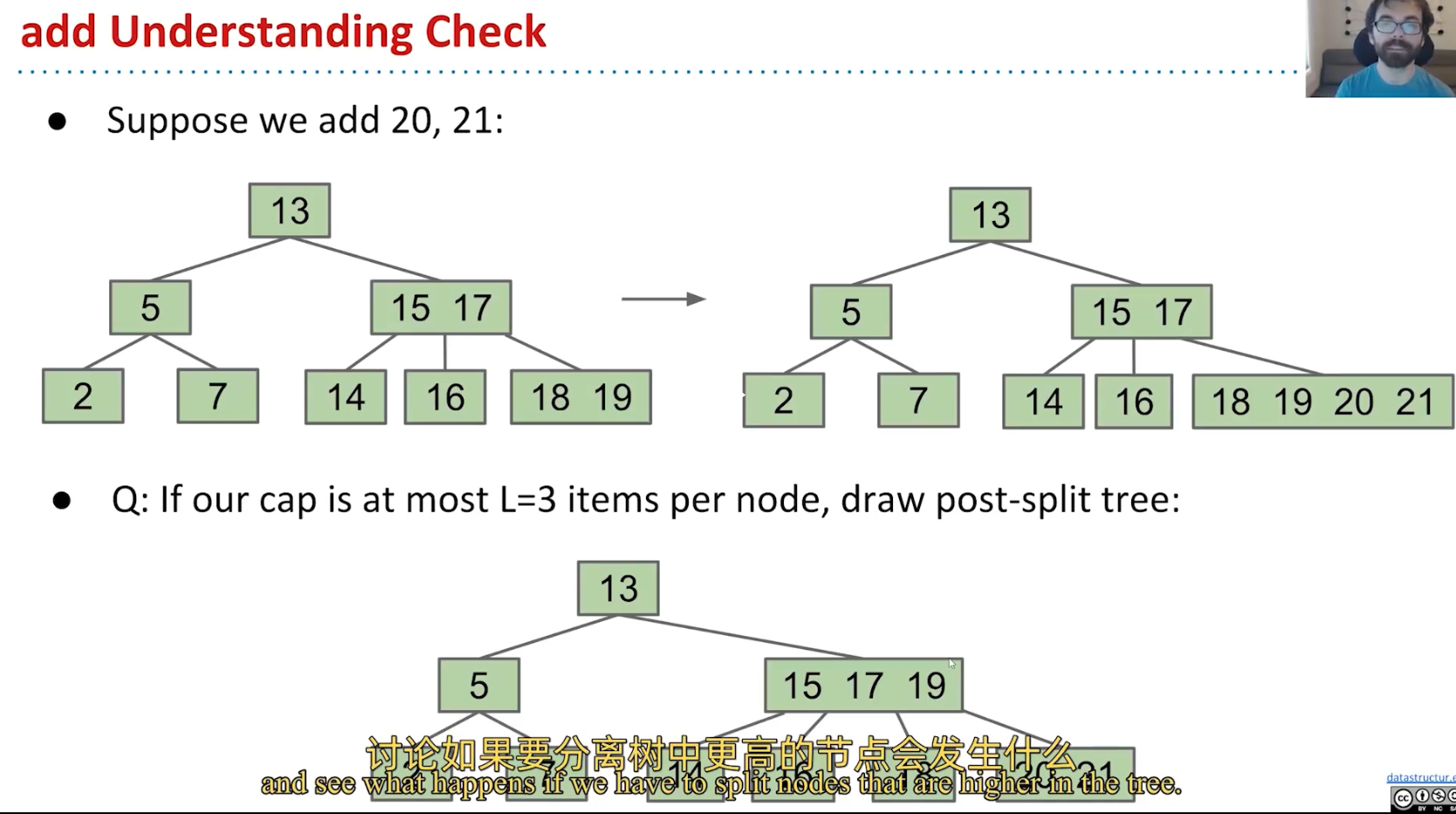
3.when no-leaf become too full:

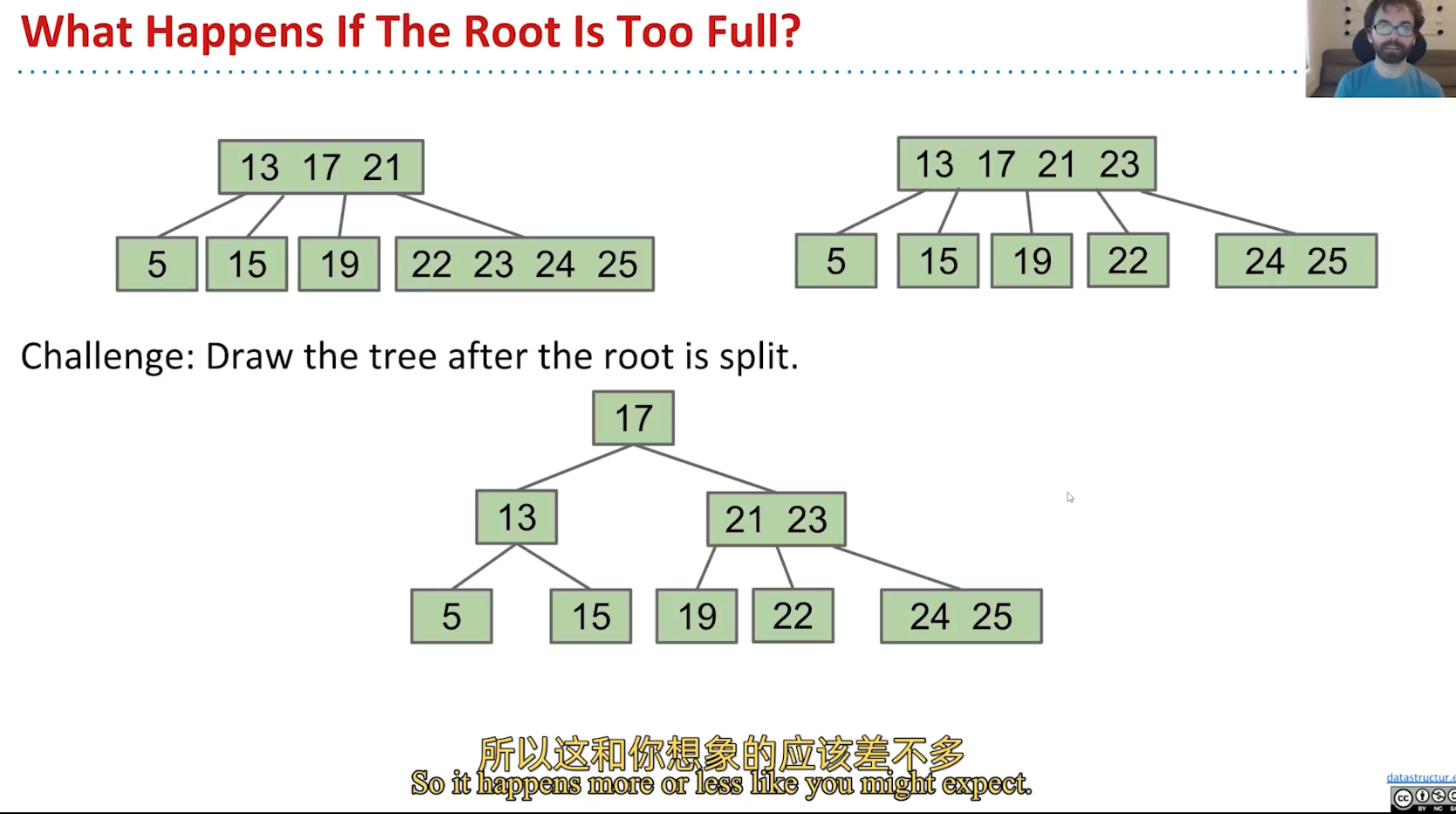
B-tree also called 2-3-4 Tree/2-4 Tree:
到此处，一直添加大值，似乎会发生只有一边会出现leaves；
Ex:L=2, insert:2,3,4,5,6,1,7 与 1,2,3,4,5,6,7 得到的是不同的树
B-Trees most popular in two context:
1.small L
2.very large L
Why B-Tree is always bushy:
B-Tree`s invariants:

1. all leaves must be same distance from source;
2. A non-leaf node with K items must have exactly K+1 children;

4.Red Black Tree

Catalan(N)?
Tree Rotation:
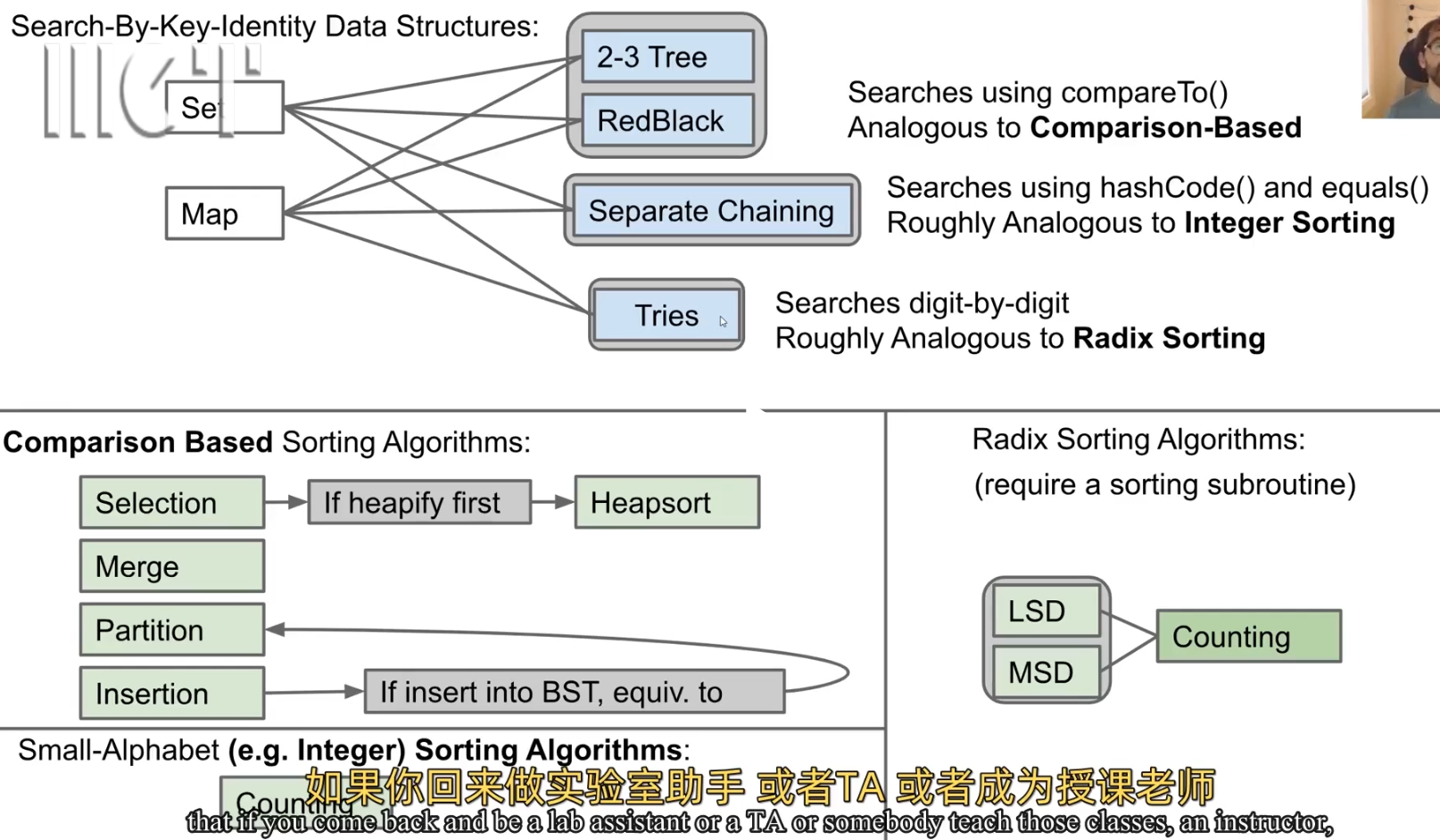
Left-Leaning Red Black Binary Search Tree (LLRB):

LLRB:Max Higeht: H+H+1

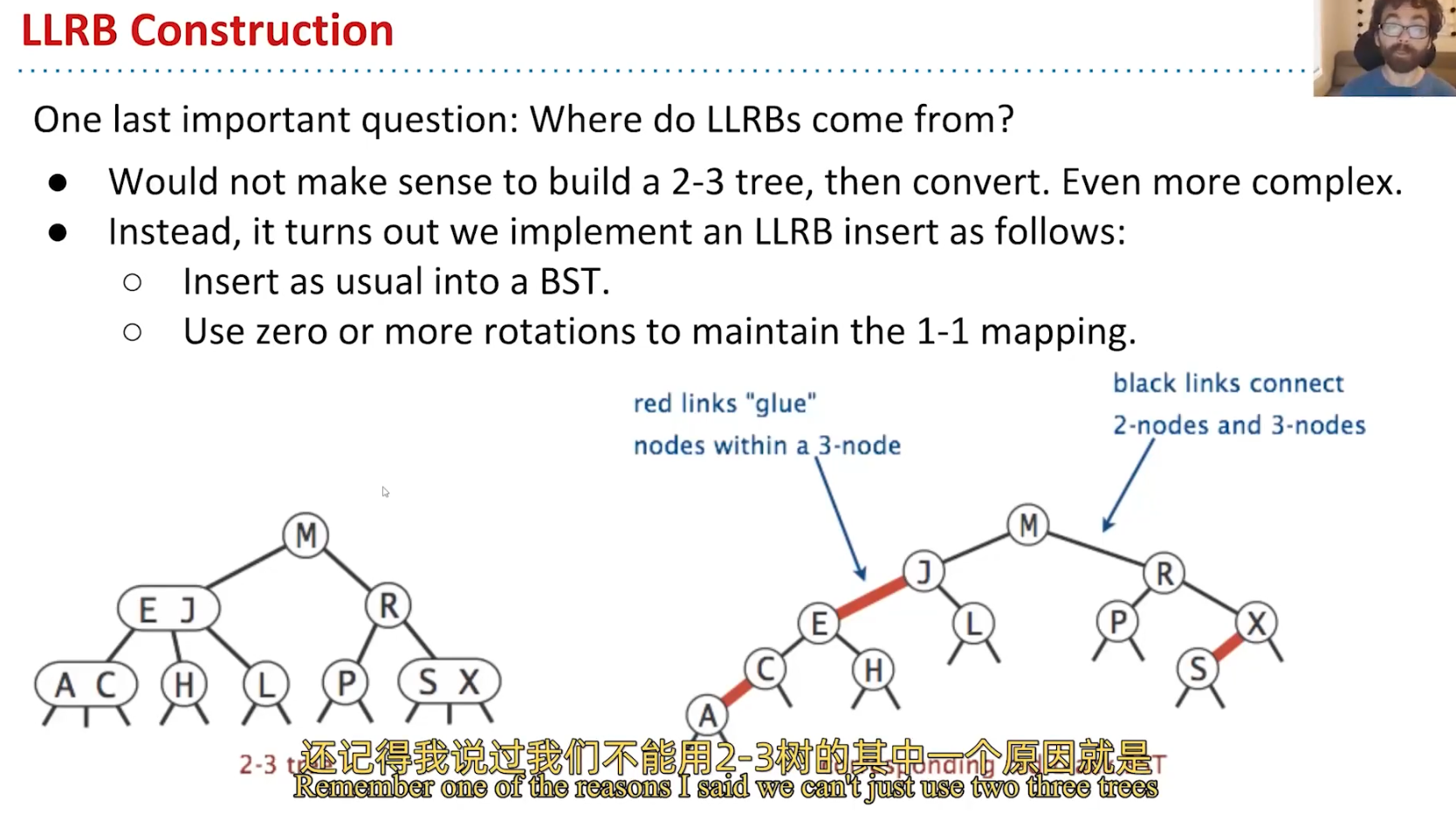
LLRB与2-3Tree 之间存在一一对应;
Red-Black Tree Insert:

5.Hash:Data Index

Using data as an index;


core question is :compute & collision
Buckets :M
Items:N
Length of list=N/M. also load factor
Operation times:1~1/M*N =O(N)
How to guarantee O(1)? N/M~1 :With increase of N also increase M;
Resize Cost: O(N);
process negative:Math.floorMod(-1,4);because -1%4=-1 in java;

Use a prime base:乘以一个基数（质数最好)以获取更好的随机性。

6.Priority Queue Interface & Heap

Queue only trace smallest element;
用法之一：节约内存，需要最大的5个，永远只需要5个位置，存放对象地址即可。
Min-Heap:
Children >=father
Complete
新增/删除 都基于这两点，新增：新增到末尾，再移动；删除：先删除root，末尾那一个移过去，再移动到正确位置。
实现树的几种方式：
Approach1:key+pointer，key+pointer[]，key+subpointer+brotherpointer;
Approach2:key[]+parents[]. Like disjoinSets;
Approach3:assume full tree, just key[],ignore parent[]；parent=(n-1)/2;left=?;right=?

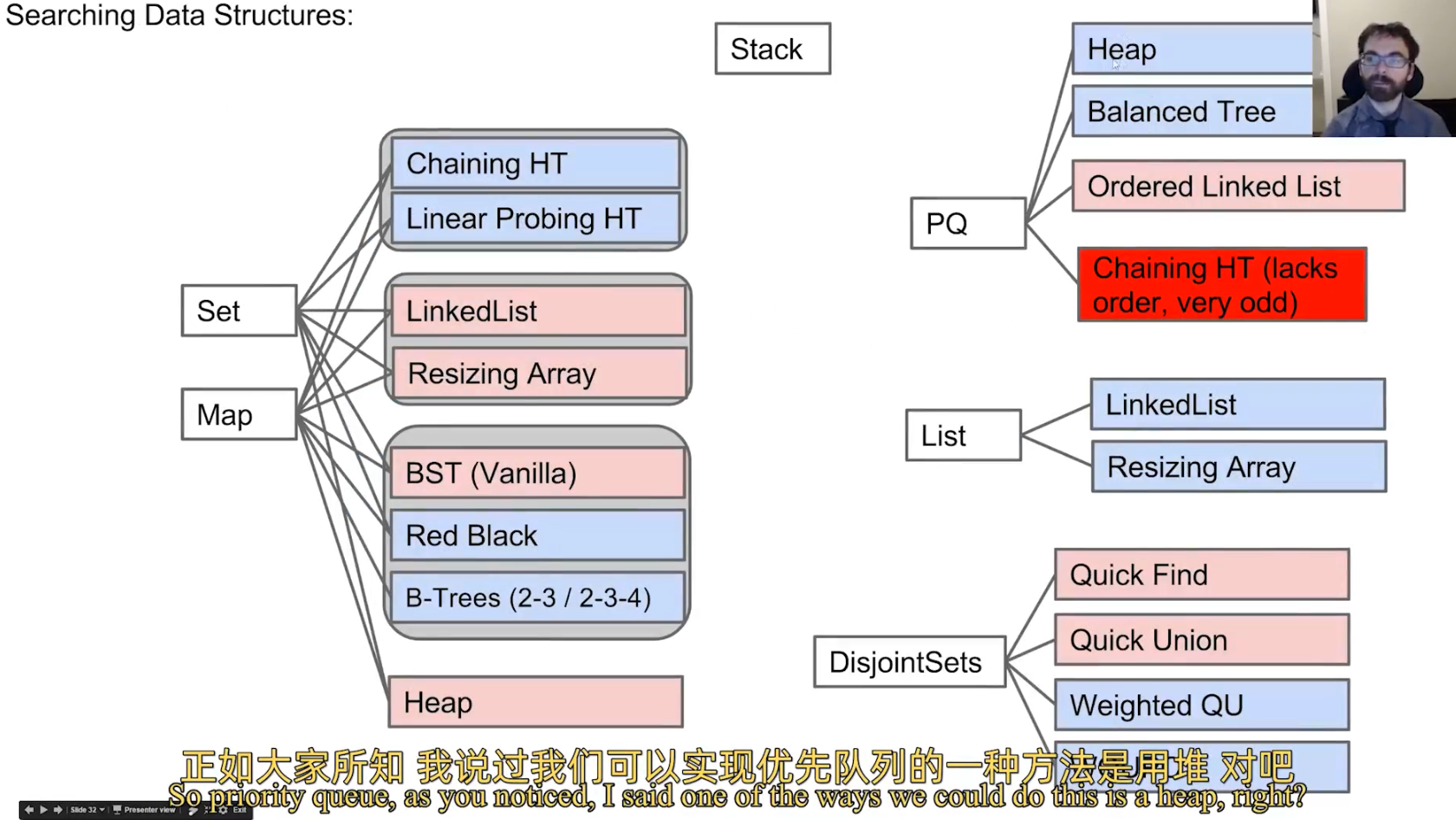
7.Search Data Structures

Search information form data;
List,Map,Set,PQ,Disjoint Sets

8.Graph

Tree are more general concept
Tree traversal:
Level Order:

1. Top-bottom;left -right

Depth Frist Traversals:

1. 3types:Preorder,Inorder,Postorder
2. Traverse deep nodes before shallow ones
3. Traversing a node is different than visit

Preorder:visit a node, then traverse childre
Inorder:traverse left, visit ,traverse right
…

打印目录：前序；统计大小：后序；
point + relation
Tree with strict hierarchical: only one path between any two nodes;
Graph with no hierarchical:one or more edges, each of which connects two nodes;
Simple graph:

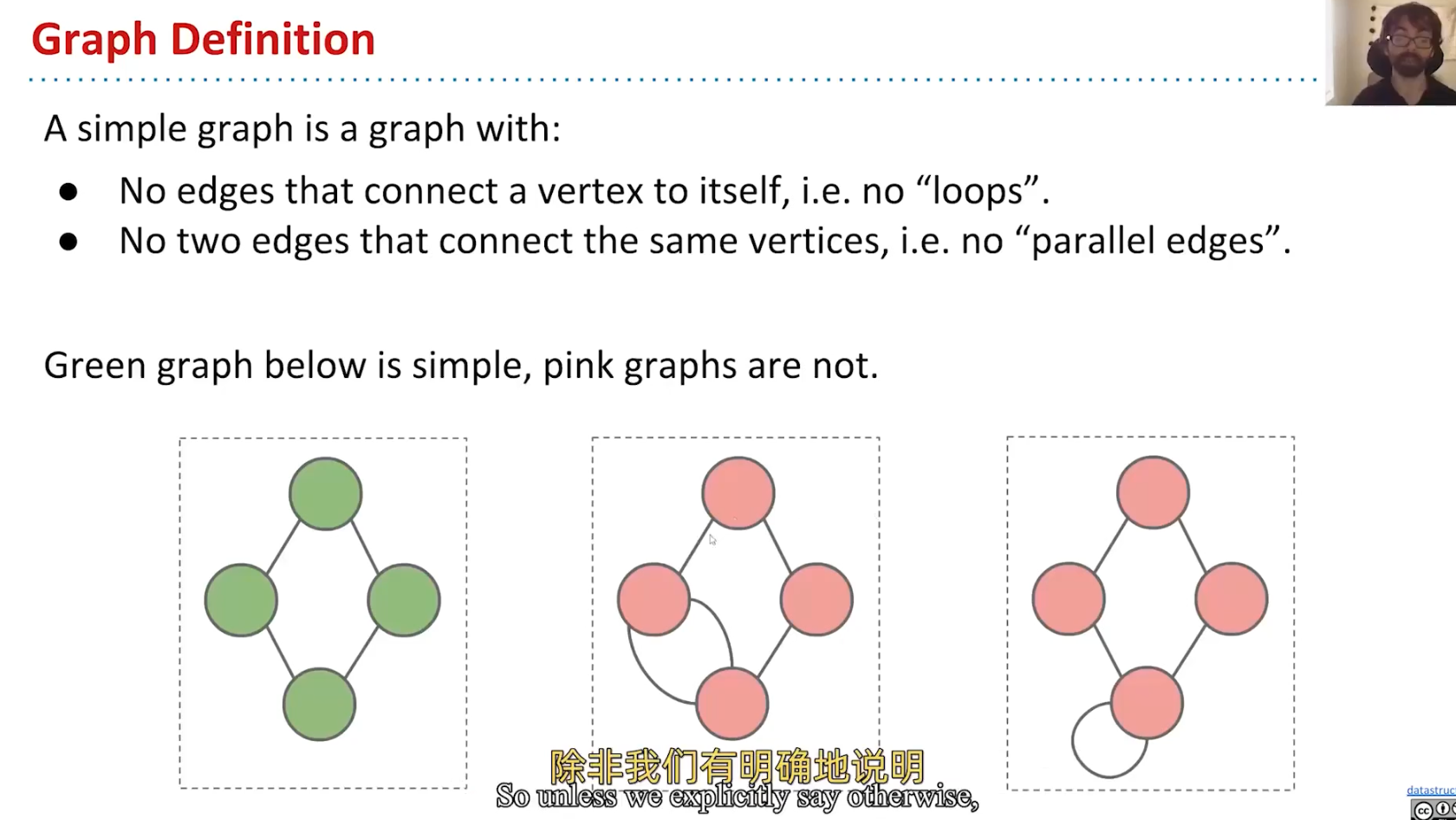
Often solve problem about graph with traversal;
s-t Connectivity:depth frist traversal;

要实现广度优先/深度优先算法，需要构建图，图api的不同，决定了最终的具体不同实现。

underling implement：
二维数组？
adjacency list：

DFS&BFS exploring graph;
Shortest Path:
Djstra
结果永远是一颗树，无向也是如此。
优先级队列+释放

9.Minimum spaning trees

如何判断一个图是否存在环？
1.DFS，排除来的点，只要找到之前已经便利过的点就存在环。
2.WeightedQuickUnionUF object

Minimum spanning tree is spanning tree of minimum total weight
only in undirected graph as subgraph:

1. is connected
2. is acyclic
3. includes all of the vertices

1&2 determine it is tree,3 makes is spanning
是否存在某个顶点，其最短路径树，恰好是该图的最小生成树？–no
最短路径树，依赖于起始节点，而最小生成树是图的属性。

计算最小生成树：
Cut Property
最小交叉边，一定是最小生成树的一部分。（边如果不是唯一的，最小生成树也可能不是唯一的）
Prim`s Algorithm 有效具体实现：

类似dj，dj关注的是到源最短的路径，prim关心树的总权重，确定保留那一条路径的偏好不同，其余基本一致。
优先级队列，移除节点时，relax到非已确定点的边，决定保留那一条边。
Kruskal`s Algorithm:
边排序，从小到大，依次添加边直到v-1（避免环）；
优先级队列
不相交集：检测环
每次添加非环的边，可以理解为两个割中取最短。

10.Range Searching and Multi-Dimensional Data

需求：最小的一个/最大的一个/范围（3～20）的数据
nearest:Tree-search
Prune: cut off tree;
如何存储多维的数据？
2D:
QuadTree:
Every node has 4 children:northwest,northeast,southwwest,southeast
Insert order decide final QuadTree;
K-D:
层级1-x,2-y,3-x,4-y xyxyxy…
Nearset:
don`t explore subspaces that can`t possible have a better answer than current;
Uniform partitioning: bucket
1-D version:Hash Table;
Multi-Dimensional Date summary:
Range Finding
Nearest
implement:
Uniform Partitioning
Quadtree
K-d Tree:K-dimensional Binary Search Tree;

11.Tries

Short for Retrieval Tree
implement:
1.Each Node have 128Array;
2.BST
3.Hash Table

12.Topological Sort

一个方法：从入度为0的节点开始 运行深度优先搜索后序，多个则重启，然后反转即我们得到的。
Depth First Search: 有时，包含重启，有时不包含重启。
Directed Acyclic Graphs
DAG SPT Algorithm:Relax in Topological Order;
DAG Longest Path Algorithm:模拟最短，赋值负数。

13.Reduction

if any subrortine for task Q can be used to solve P ,we say P reduces to Q;
(Karp and Cook reductions)

14.Sort

三角性：a>b a=b a<b. 有一个为真
传递性：。。。

选择最小排序 n平方–堆排序nlogn（放到堆里面再取出来）–in-plance heap sort
数组堆化？？
归并排序
插入排序(类似最小选择排序)：
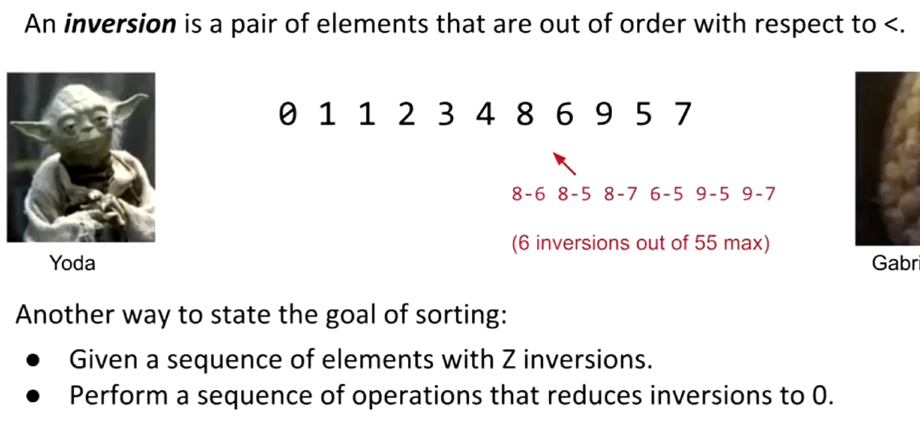
可以理解为，消灭inversion。（三角形，理想O(N),worst O(N平方)）
插入排序的消耗与inversion成比例
一般需要排序的数量小于15 插入排序是最快的，arrays.sort() 使用的归并排序，数量小于15就切换为插入排序。
终极王者：quick sort

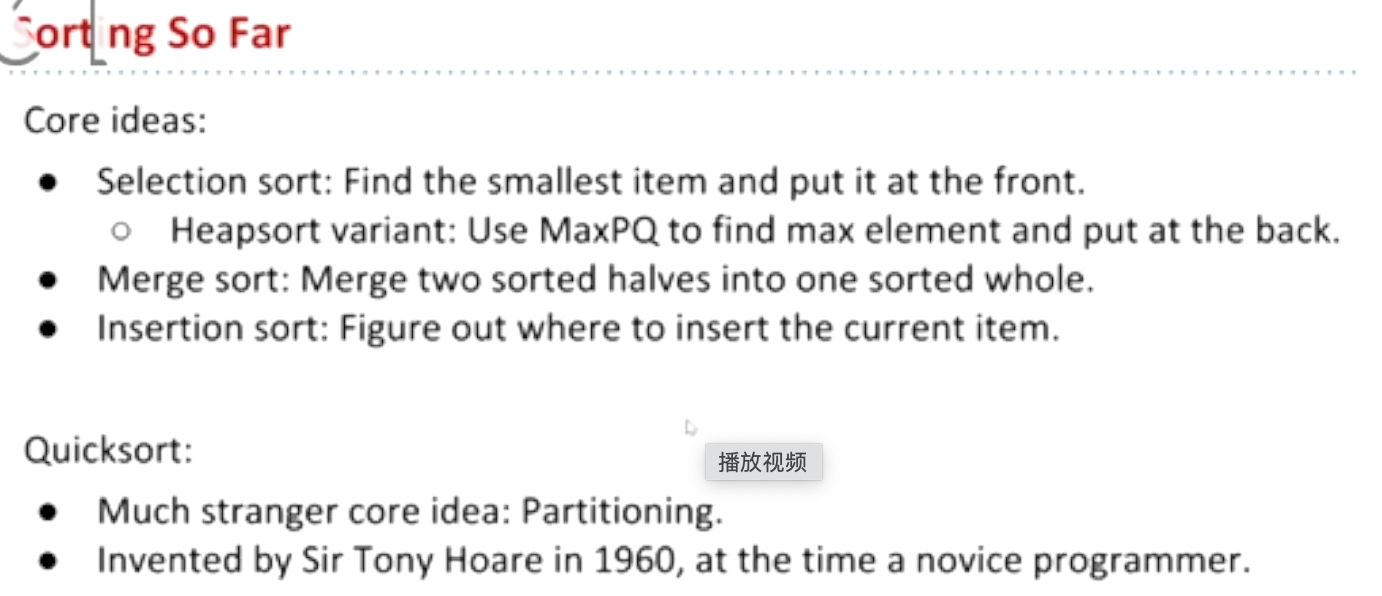
选一个标记，分区，然后再对分区进行分区。
快速排序–BST sort
n平方～nlongn。受到所选择元素（主元）的位置影响，随机试验是接近nlogn。
很难理论上证明快速排序比归并排序快，但经验如此。

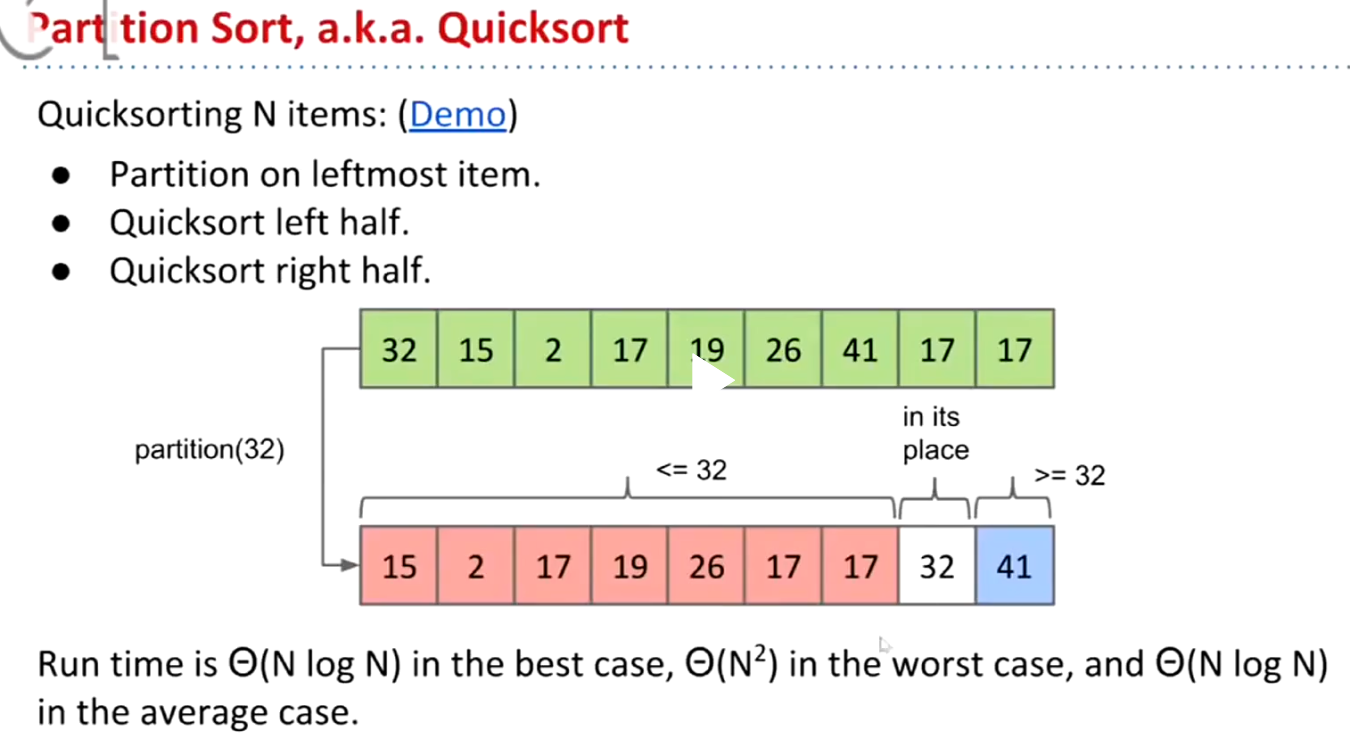
avoid the worst case:


Heap sort:很少被使用。
one quick sort implement (random):

Another implement (smart pivot):

However Quick Select : partition

Arrays.sort
TimSort


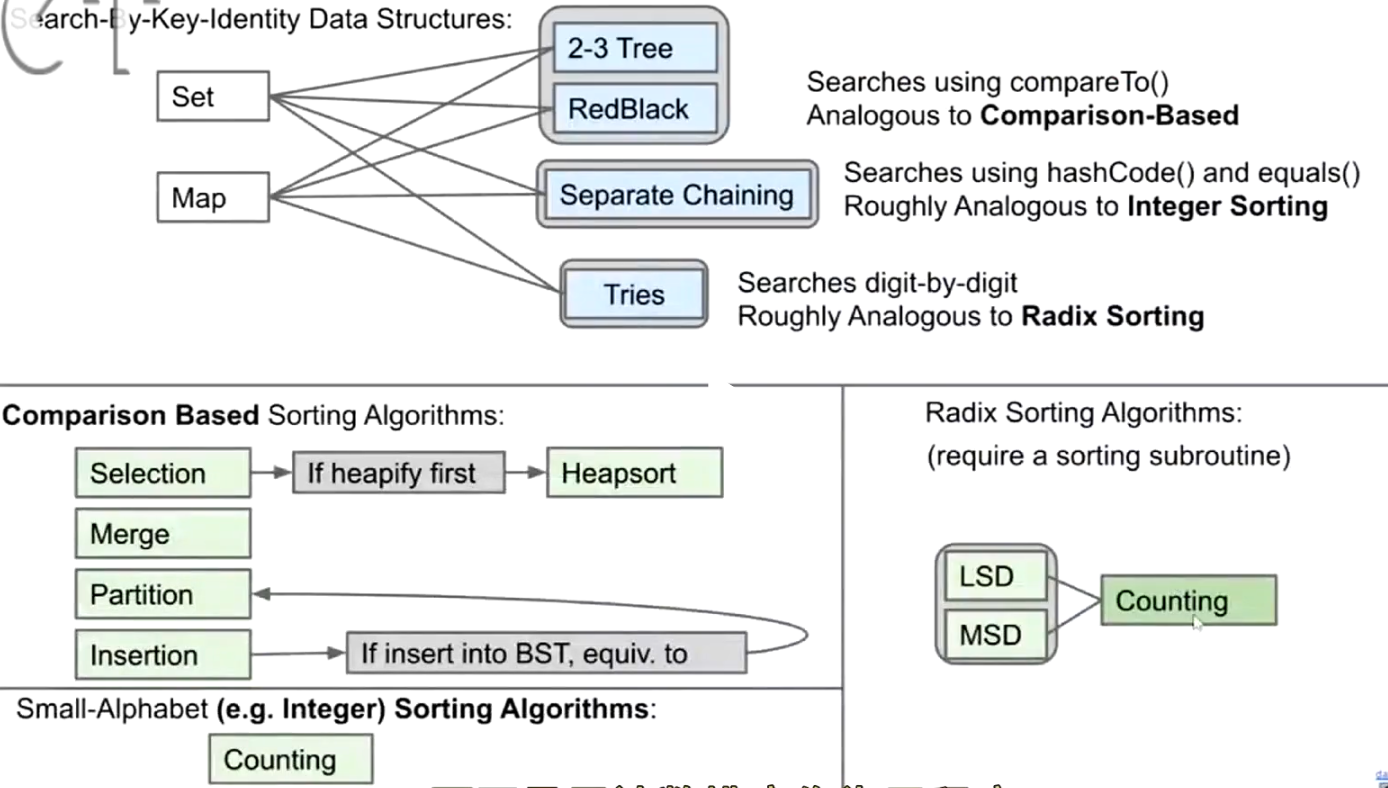
more information of sort:
几个数学例子：
N!>N/2的N/2次方。
log(N!)>NlogN;
puppy-cat-dog，需要多少信息可以确定三个的顺序？
假设4个：一共用4!=24种可能排序，一颗完全二叉树需要多少层才能有24个叶子？log2（24）～5
决策树：log(N!)个问题，neraly：nlogn
任何基于比较的排序，需要nlogn 次比较。
radix sort
sleep sort – genre counting sort(alphabet keys only) – radix sort

对 counting sort 的扩展 推广到非alphabet范围：radix sort
LSD Radix Sort: 最低有效位排序。w（n+r）
MSD Radix Sort:最高有效位排序。n+r 到 w（n+r）， 分组
归并排序vs基数排序msd:
100字符串，每个1000个字符：
msd:1000n
merged sort：1000nlogn
从比较的支付而言，mergesort更多，但实验下来，mergesort更快
cost model not well ， just-in-time complier （slid&lecture demo）
关掉优化 vm-option xint。merge sort slower
compare integer in radix sort，注意进制